Quantum mechanics, as developed by Erwin Schrodinger in 1926, is based on the wave motion associated with the particles. For the wave motion of the electron in the three dimensional space around the nucleus, he put forward an equation known as Schrondinger wave equation.
where ψ is the amplitude of the wave where the coordinates of the electrons are ( x,y,z) ,E is the total energy of the electron, V is its potential energy, m is the mass of the electron and h is the Planck’s Constant,
represents second derivative of Ψ w.r.t. x.
In short Schrodinger wave equation is written as
Where H is a mathematical operator ,called Hamiltonian operator.
The solution of Schrodinger wave equation for an electron in an atom gives the value of E and Ψ .The value of E represents the quantised value of energy which the electron in the atom can have. The corresponding value of ψ are called wave functions.
Significance of the wave function
In case of light or sound, the square of the amplitude of the wave at any point gives the intensity of the sound or light at that point, Similarly the square of the amplitude of the electron wave ie ψ2 at any point gives the intensity of the electron wave at that point which in view of Heisenberg Uncertainty Principle means probability of finding the electron at that point.
ψ2 at any point gives the probability of finding the electron at that point i.e. electron density at that point.
The region around the nucleus which represents the electron density at different points is called an orbital.
The wave function for an electron in an atom is called orbital wave function or atomic orbital. Since an electron can have any wave function ,therefore, there are many atomic orbitals in an atom.
Probability provides the best possible description of a situation which cannot be described with certainty.
The electron spends most of its time in the volume of Sphere bounded by that distance and for rest of the time, the electron can be found outside the volume of the sphere.
The region of space around the nucleus which describes the probability of finding an electron of given energy in terms of dots is called an electron cloud.
An atomic orbital may be defined as the three dimensional space around the nucleus within which the probability of finding an electron of given energy is maximum.
Features of quantum mechanical model of atom
1)The electrons in an atom have only quantized value of energy.
2)These quantized values of energy are obtained from the solution of Schrodinger Wave Equation. The values of the wave function Ψ are also obtained from the solution of Schrodinger Wave Equation.
3)The wave function Ψ is simply a function of coordinates of the electron and has no physical significance as such.ψ2 give the probability of finding the electron at that point i.e. electron density at that point.
4) By finding ψ2 at different points around the nucleus in an atom, we can predict the region of space around the nucleus within which the probability of finding the electron with a definite value of energy is maximum. This space around the nucleus is called orbital .Wave function Ψ is called orbital wave function or atomic orbital.
5) Since an electron can have many wave function therefore there are many atomic orbitals in an atom.
6)The orbital wave function contains all the information about an electron in an atom and the quantum mechanics helps to extract this information.
Application of Schrodinger Wave Equation to hydrogen atom
When Schrodinger Wave Equation is solved for hydrogen atom, the solution gives possible values of the energy ( E ) .
These values of energy corresponds to the energy levels which the electron in an atom can occupy.
These values of energy are called eigen values.
The corresponding values of wave functions ( Ψ ) are called eigen functions.
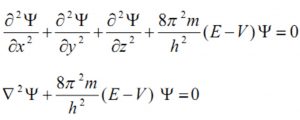
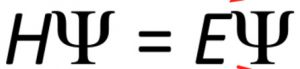
Thanks For such a good answer
It was very helpful………… Thank you
Thank you so much. Its very useful…..
Thanks a lot for such a fantastic answer
..
THANK YOU…..
wonderful information
please keep it up
The best long answer for this question ever
Thank you so much