Shapes of Atomic Orbital

An orbital is the region of space around the nucleus within which the probability of finding an electron of given energy is maximum.

The probability at any point around the nucleus is calculated using schrodinger wave equation and is represented by the density of the points.

Shape of s orbital

For the coordinates( x, y, z) of the electron with respect to the nucleus, schrodinger Wave equation can be solved to get the values of the orbital wave function ψ. But Ψ has no physical significance. The square ψ²  has the significance as it gives the electron probability density of the electron at that point.

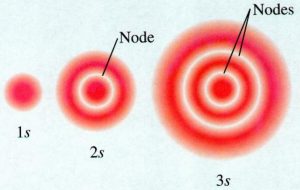
1) The probability of 1s electron is found to be maximum near the nucleus and decreases as the distance from the nucleus increases.

2) In case of 2s electrons, the probability is again maximum near the nucleus and then decreases to zero and increases again and then decreases as a distance from the nucleus increases.

3) The intermediate region where probability is zero is called nodal surface or node.

2s orbital differ from 1s orbital in having node within it.3s has two nodes.Any ns orbital has ( n-1) nodes.

 

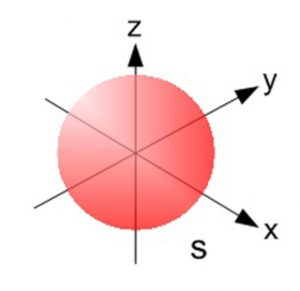
1) The probability of finding the electron belonging to a s orbital of any main shell is found to be identical in all directions at a given distance from the nucleus. Hence s – orbital is spherical in shape which is symmetrical around the nucleus.

2) For s orbital azimuthal quantum number l = 0. Magnetic quantum number m is also equal to 0.s orbital has only one orientation. The only shape having one orientation is a sphere. s orbital is spherical in shape.

1s, 2s, 3s etc all have spherical shape, they differ in:

1) the number of nodes

2) size and energy. These increases with increase in principal quantum number, n.

Shapes of P orbital

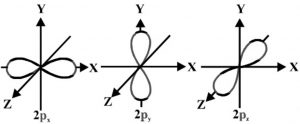
It is found that the probability of finding the electron is maximum in two lobes on the opposite side of the nucleus. This gives rise to dumb-bell shape for the p orbital.

The probability of finding a particular P electron is equal in both the lobes. There is a plane passing through the nucleus on which the probability of finding the electron is almost zero. This is called a nodal plane.

For p orbital l= 1, m = -1, 0, +1 .Thus  p orbital has three different orientation designated as p_x, p_y, p_z  depending upon whether the electron density is maximum along the x-axis,  y axis and Z axis.

P orbital have directional characteristics and hence are helpful in predicting the shape of molecules.

As n increases these p orbitals become larger in size and have higher energies. The three p orbitals belonging to a particular energy shells have equal energies and are called degenerate.

Shapes of d orbital

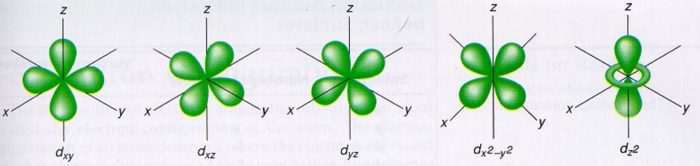
For d orbital, l=2.Hence m= -2, -1, 0, +1, +2

There are 5 d orbitals, depending upon the axes along which or between which their electron clouds are concentrated, their names and shapes are:

 

d _z² has a doughnut shaped electron cloud in the centre whereas  others clover leaf shape.

Number of nodes in any orbital= (n – l -1)