Gibbs Free Energy

Another thermodynamic quantities that helps in predicting the spontaneity of a process is Gibbs free energy or Gibbs energy of Gibbs function.

It is denoted by G and is given by the equation

G=H -TS

where H is the heat content ,T is the absolute temperature and S is the entropy of the system.

G₁ = H₁ -TS₁ for the initial state

G₂ = H₂ -TS₂ for the final state

G₂ -G₁ =( H₂ -H₁) -T (S₂ -S₁)

ΔG = ΔH -TΔS

ΔG =G₂ -G₁  is the change in Gibbs free energy of the system

ΔH= H₂ -H₁ is the enthalpy change of the system

ΔS =S₂ -S₁ is the entropy change of the system.

ΔG = ΔH -TΔS is known as Gibbs – Helmoholtz equation.

Gibbs free energy is that thermodynamic quantity of a system the decrease in whose value during a process is equal to the maximum possible useful work that can be obtained from the system.

The relationship between heat absorbed by a system q, the change in its internal energy , ΔU , and the work done by the system is given by the equation of the first law of thermodynamics i.e.

q= ΔU + w_expansion + w_{non-expansion}

Under constant pressure conditions , the expansion work is given by PΔV.

 

q= ΔU + PΔV  + w_{non-expansion}

q = ΔH + w_{non-expansion}

For a reversible change taking place at constant temperature ,

ΔS = q_rev /T

q_rev =TΔS

TΔS = ΔH + w_{non-expansion}

ΔH – TΔS = – w_{non-expansion}

For a change taking place under condition of constant temperature and pressure,

ΔG = ΔH -TΔS

ΔG = – w_{non-expansion}

Free energy change can be taken as a measure of work other than the work of expansion.

The work of expansion cannot be converted to other useful work ,whereas the non – expansion work is convertible to useful work.

−ΔG = w_{non-expansion} = w_useful

The decrease in free energy of system during any change, ΔG,  is a measure of the useful or net work derived during the change. The free energy, G, of a system is a measure of its capacity to do useful work. It is a part of the energy of the system which is free for conversion to useful work and is therefore called free energy.

The free energy change is equal to the maximum possible useful work that can be obtained from the process. Hence we can write,

−ΔG = w_max

The greater the change in Gibbs energy , greater is the amount of work that can be obtained from the process.

If the work involved is the electrical work then as electrical work = nEF , the above relationship is written as:

−ΔG = nEF

where n = number of electrons involved in the cell reaction

E= EMF of the cell

F =Faraday

If all the reactants and products of the cell reaction are in their standard states i.e. 298 K and one atmosphere pressure, the above relation is written as

−ΔG° = nFE°

where ΔG° is the standard free energy change,

ΔG° is the standard EMF of the cell.

In a fuel cell, it is found that the heat evolved is not completely converted into energy i.e. useful work.

The ratio ΔG / ΔH is called the efficiency of the fuel cell.

 

Spontaneity in terms of Free energy change

1)Deriving the criteria from entropy consideration

The total entropy change when the system is not isolated from the surrounding is given by

ΔS = ΔS_system + ΔS_surrounding

Consider a process being carried out at constant temperature and pressure. Suppose the heat is lost by the surrounding and gained by the system.If the heat lost by the surrounding is represented by q_p then by definition of entropy change

ΔS_surrounding = − q_p /T

At constant pressure,

q_P = ΔH

ΔS_surrounding = − ΔH /T

ΔStotal =  ΔS_system − ΔH /T

ΔS_total =  ΔS − ΔH /T

Multiplying throughout by T ,we get

TΔS_total = TΔS – ΔH

ΔG = ΔH -TΔS

TΔS_total = – ΔG

ΔG =  − TΔS_total 

1) If ΔS_total is positive, the process is spontaneous .

2) If ΔS_total is zero, the process is in equilibrium.

3) If ΔS_total is negative ,the direct process is non spontaneous, the reverse process may be spontaneous.

The criteria in terms of free energy change for the spontaneity of the process will be as follow:

1) If ΔG is negative, the process will be spontaneous.

2) If ΔG is zero, the process is in equilibrium.

3)If ΔG is positive, the direct process is non spontaneous, the reverse process may be spontaneous.

 

2)Driving the criteria from Gibbs energy equation

According to Gibbs energy equation,

ΔG = ΔH -TΔS

This equation combines in itself the factors which decides the spontaneity of a process, namely:

1)the energy factor, ΔH

2)the entropy factor, TΔS

ΔG is the resultant of energy factor and entropy factor.

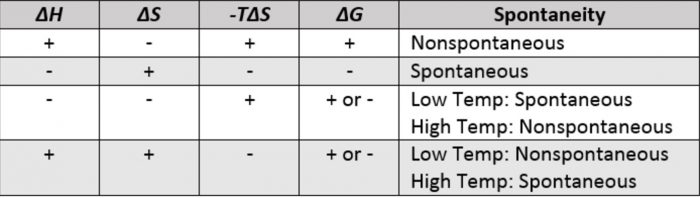
Depending upon the signs of ΔH and TΔS and their relative magnitude, the following possibilities arises:

1) When both ΔH and TΔS are negative i.e. energy factors favours the process but randomness factors opposes it. Then

1) If ΔH > TΔS the process is spontaneous and ΔG is negative.

2) If ΔH < TΔS the process is non spontaneous and ΔG is positive.

3) If ΔH = TΔS, the process is in equilibrium and ΔG is zero.

2) When both ΔH  and TΔS are positive i.e. energy factor opposes the process but randomness factor favours it. Then

1) If ΔH > TΔS the process is non-spontaneous and ΔG is positive.

2) If ΔH < TΔS the process is spontaneous and ΔG is negative.

3) If ΔH = TΔS, the process is in equilibrium and ΔG is zero.

3) When ΔH is negative and TΔS is positive i.e. energy factor as well as the randomness factor favour the process. The process will be highly spontaneous and ΔG will be highly negative.

4) When ΔH is positive but TΔS is negative i.e. energy factor as well as the randomness factor opposes the process. The process will be highly non-spontaneous and ΔG will be highly positive.

1) If ΔG is negative the process is spontaneous.

2) If ΔG is zero, the process does not occur or the system is in equilibrium.

3) If ΔG is positive the process does not occur in the forward direction. It may occur in the backward direction.

Effect of temperature on the spontaneity of a process

The spontaneity of a process depends upon

1) the energy factor

2) the randomness or entropy factor

The resultant ΔG = ΔH – T ΔS would change with temperature and so would spontaneity of the process.

 

For endothermic reactions

ΔH is always positive i.e. this factor opposes the process.

1) If TΔS is negative, this factor will also oppose the process and process will be non spontaneous.

2) If TΔS is positive then the process can occur if magnitude of the factor TΔS is greater than the magnitude of ΔH. The reaction is then said to be entropy driven. The magnitude of the factor,TΔS is affected by temperature as follow:

1) If the temperature is very low such that TΔS < ΔH in magnitude, ΔG will be positive and hence the process will be non spontaneous.

2) If the temperature is moderate such as TΔS > ΔH slightly in magnitude , ΔG will be slightly negative. Hence the process will be spontaneous but slow.

3) If the temperature is high, TΔS will be much greater than ΔH in magnitude so that ΔG is highly negative. Hence the process will not only be spontaneous but fast.

An endothermic reaction which may be non-spontaneous at low temperature may become spontaneous at high temperature.

This is the reason why endothermic reactions are carried out at high temperature.

For exothermic reaction

ΔH is always negative i.e. this factor always favours the process.

If  TΔS is positive , this factor will favour the process and the process will always be spontaneous.

If TΔS is negative, then the process can occur only if the magnitude of ΔH is very large so that ΔG is negative. The reaction is then said to be enthalpy driven.

The magnitude of TΔS and hence, the spontaneity of the reaction is affected by temperature as follow :

1) If the temperature is so high that TΔS > ΔH in magnitude, ΔG will be positive and the process will be non- spontaneous.

2) If the temperature is made so low that TΔS < ΔH  in magnitude, ΔG will be negative and the process will be spontaneous.

An exothermic reaction which may be non-spontaneous at high temperature may become spontaneous at low temperature.

 

Standard free energy change of a reaction (ΔG° _reaction )and standard free energy of formation(Δ_fG°)

Standard free energy change of a reaction is defined as the change in free energy which takes place when the reactants in the standard state are converted into products in their standard state.

The free energy change during a process can be calculated from the standard free energy of formation of the different reactants and products involved, taking standard free energy of formation of elements as zero i.e. for any process or reaction,

Δ_rG° = ( sum of the standard free energy of formation of products) – ( Sum of the standard free energy of formation of reactants)

Δ_rG° = ∑Δ_fG°( products) –  ∑Δ_fG°(Reactants)

Standard free energy of formation of a compound is defined as the free energy change which take place when one mole of the compound is formed from its elements taken in their standard state.

Standard free energy of formation of elementary substances is taken as zero.

Free energy change and chemical equilibrium

A reaction is spontaneous if ΔG is negative. In a reversible reaction, the forward as well as backward reaction takes place. ΔG is negative for the forward as well as for the backward reaction.

The free energy change of the reaction in any state ΔG is related to the standard free energy change of the reaction,ΔG° according to the equation

Δ_rG = Δ_rG° + RT lnQ

where Q is the reaction quotient. It is equal to Q_p if the products and reactants are gaseous and equal to Q_c if they are in the solution.

When equilibrium is attained, there is no further free energy change i.e.  ΔG =0 and Q becomes equal to K.

0 = Δ_rG° + RT lnQ

Δ_rG° = − RT lnQ

Δ_rG° = −2.303 RT log K

K = e^-Δ_rG°/RT

 

Magnitude of equilibrium constant for exothermic and endothermic reaction

According to Gibbs energy equation,

Δ_rG° = Δ_rH° – T Δ_rS°

RT ln K = T Δ_rS° – Δ_rH°

ln K = (  T Δ_rS° – Δ_rH° ) / RT

For strongly endothermic reaction, ΔH° is large and positive.Hence the term on the right hand side have a small value and so will be ln K and hence K.

For strongly exothermic reaction, ΔH° is large and negative.Hence the term on the right hand side will have large value and so will be ln K and hence K.

Third law of thermodynamics

The entropy of a pure substance increases with increase of temperature because molecular motion increases with increase of temperature.

Entropy decreases with increase of temperature.

The entropy of a perfectly crystalline solid approaches zero as the temperature approaches absolute zero.

or

The entropy of all perfectly crystalline solids may be taken as zero at absolute zero of temperature.

or

At absolute zero, a perfectly crystalline solid has a perfect order of its constituent particles , i.e.  there is no disorder at all. Hence the absolute entropy is taken as zero.

The entropy per mole of the substance under standard conditions at the specified temperature is called standard molar enthalpy or absolute entropy.

Residual entropy

There are certain substances which possess some entropy even at absolute zero.The Entropy possessed by a substance at absolute zero is called residual entropy.

Knowing the standard entropies of the different reactants and products involved, entropy change of a reaction can be calculated using the equation :

ΔS° = ( sum of the standard absolute entropies of products) – ( Sum of the standard absolute entropies of reactants)

ΔS= ∑S°( products) –  ∑S°(Reactants)

Standard entropy of formation of a compound is defined as the entropy change that takes place when 1 mole of the compound in the standard state is formed from its elements also taken in the standard state.