Werner Heisenberg, a German physicist, in 1927 gave a principle about the uncertainty in simultaneous measurement of position and momentum of small particles.
Heisenberg’s uncertainty Principle states that:
It is impossible to measure simultaneously the position and momentum of a small particle with absolute accuracy or certainty. The product of the uncertainty in the position ( Δx ) and the uncertainty in the momentum(Δp) is always constant and is equal to or greater than h/4π, where h is the Planck’s Constant ie.
Significance of Heisenberg Uncertainty Principle
Heisenberg’s uncertainty Principle holds good for all objects but it is significant only for microscopic particles. The energy of the photon is insufficient to change the position and velocity of bigger bodies when it collides with them.
For a particle of mass 1 mg, we have
Δx . Δv = h / 4π m
Δx . Δv = 6.626 × 10-34 / 4 × 3.1416 × ( 106 )
Δx . Δv = 10-28 m2 s-1
The product Δx and Δv is extremely small. For particle of mass greater than 1 mg, the product will be still smaller. Hence these values are negligible.
For a microscopic particle like an electron, we have
Δx . Δv = 6.626 × 10-34 / 4 × 3.1416 × ( 9.11 × 10-31)
Δx . Δv = 10-4 m2 s-1
If uncertainty in position is 10-4 ,uncertainty in velocity will be 0.1 m/s.
Bohr’s concept of fixed circular path with definite position and momentum of electron have been replaced by stating that the electron has the probability of having a given position and momentum.
Electron cannot exist in the nucleus
This is because the diameter of the atomic nucleus is of the order 10-15 m. If the electron were to exist within the nucleus, the maximum uncertainty in its position would have been 10-15 m .Taking the mass of electron as 9.1 × 10 -31kg, the minimum uncertainty in velocity can be calculated by applying uncertainty Principle as follow:
Δ x . Δ p = h/4π
Δ x. (m × Δv) = h/4π
Δ v = h/ 4π × Δx × m
Δ v = 6.626 × 10-34 / 4 × 3.1416 × 10-15 × 9.1 × 10 -31
Δ v = 5.77 × 1010 m/s
This value is much higher than the velocity of light ( 3 × 108 )and hence is not possible.
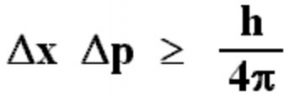
It is very helpful.
Thanks renu
That’s really helpful
Thanks alot mam