A gas which obeys the ideal gas equation, PV = nRT under all conditions of temperature and pressure is called an ideal gas.
There is no gas which obeys the ideal gas equation under all conditions of temperature and pressure.
The gases are found to obey the gas laws if the pressure is low or the temperature is high. Such gases are known as real gases.
It is found that gases which are soluble in water or are easily liquefiable show larger deviation than gases like H2, O2, N2 etc.
Deviation from ideal behaviour
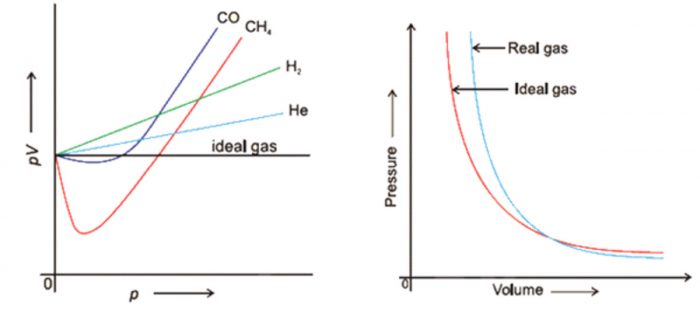
According to Boyle’s law , PV = constant at constant temperature. Hence , at constant temperature ,plot of PV vs P should be a straight line parallel to x-axis.
For gases like H2 and He ,PV increases continuously with increase of pressure whereas for gases like CO , CH4, PV first decreases with increase of pressure and reaches a minimum value and then increases continuously with increase of pressure.
If we plot experimental value of pressure versus volume at constant temperature and theoretically calculated values from Boyle’s Law, the two curves do not coincide.
The extent to which a real gas deviates from ideal behaviour can be studied in terms of Compressibility factor.
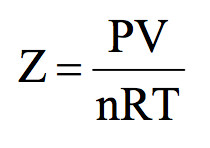
negative deviation,
1) For ideal gases , Z =1 , PV =nRT
2) For real gases , Z≠ 1 , PV ≠ nRT
a) When Z < 1 , the gas is said to show negative deviation. This implies that the gas is more compressible than expected from ideal behaviour.
This is also attributed to predominance of attractive forces among the molecules of these gases.
b) When Z > 1, the gas is said to show positive deviation. This implies that the gas is less compressible than expected from ideal behaviour.
This is attributed to predominance of strong repulsive forces among the molecules.
Greater the departure in the value of Z from unity, greater are the deviation from ideal behaviour.
At the same temperature and pressure, the extent of deviation depends upon the nature of the gas.
For the same gas, at a particular pressure, the extent of deviation depends upon the temperature. As the temperature increases, the minimum in the curve shifts upwards. A temperature is reached at which the value of Z remains close to 1 over an appreciable range of pressure.
The temperature at which a real gas behaves like an ideal gas over an appreciable pressure range is called Boyle temperature or Boyle point.
At ordinary pressure, Z is very near to 1 i.e. the deviation from ideal behaviour are so small that the ideal gas laws can be applied.
Significance of compressibility factor
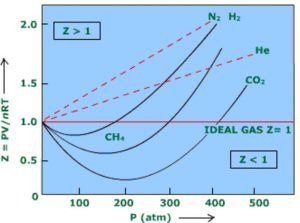
Z = PVreal / nRT
If the gas shows ideal behaviour,
PVideal = nRT
Videal = nRT/P
Z = Vreal / Videal
Compressibility factor is the ratio of the actual molar volume of the gas to the calculated molar volume at the same temperature and pressure.
Cause of Deviation form ideal behaviour
The real gases obey ideal gas equation only if the pressure is low or the temperature is high.If the pressure is high or temperature is low, the real gases show marked deviation from ideal behaviour.
At high pressure or low temperature, the following two assumptions of Kinetic theory of gases are faulty:
1)The volume occupies by the gas molecules is negligible as compared to the total volume of the gas.
2)The force of attraction or repulsion between the gas molecules are negligible.
If the pressure is high or the temperature is low, the gas molecules come close together. Hence under these conditions:
1)The forces of attraction or repulsion between the molecules may not be negligible.
2)The volume occupied by the gas may be small that the volume occupied by the molecules may not be negligible.
Van der Waals Equation
J.D. van der waal in 1873 , modified the ideal gas equation by applying correction so as to take into account
1)The volume of the gas molecules
2)The forces of attraction between the gas molecules
Van der waal equation for 1 mole of the gas,
Van der waal equation for n mole of the gas,
where a and b are called van der waal constants.Their value depend upon the nature of gas.
Derivation of Van der waals equation
Correction for Volume
Corrected volume = (V – b) for one mole
= ( V – nb) for n moles
Correction for pressure
A molecule lying within the vessel is attracted equally by other molecules on all sides but a molecule near the wall is attracted by the molecules inside. Hence it exerts less pressure. Observed pressure is less than the ideal pressure.
Corrected pressure = p + P
d ∝1/V
d ∝ n/ V for n moles
p ∝ 1/ V2
p = a / V2 for one mole
p ∝ n2 / V2 for n moles
p = an2 / V2 for n moles
Corrected pressure = (P + a/V2) for one mole
Corrected pressure = (P + an2/V2) for n mole
Substituting the corrected values of volume and pressure in the ideal gas equation , we get
Significance of Van der waal constant
van der waal constant a: Its value is a measure of the magnitude of the attractive forces among the molecules of the gas. Greater the value of A ,larger are the intermolecular forces of attraction.
van der waal constant b: Its value is a measure of the effective size of the gas molecules. Its value is equal to four times the actual volume of the gas molecule. It is called excluded volume or co-volume.
Units of Van der waals constant a
Units of Van der waals constant b
Behaviour of real gases by van der waals equation
1) At very low pressure
V is very large. Hence, the correction term a/V2 is so small that it can be neglected. The correction term b can also be neglected in comparison to V. Thus van der waals equation reduces to the form PV = RT
2) At moderate pressure
At moderate pressure, V decreases. Hence a / V2 increases and cannot be neglected. V is still large enough in comparison to b so tht b can be neglected. Thus , van der waals equation becomes
(P + a/V2) V = RT
PV + a/V = RT
PV =RT – a/V
PV / RT = 1 – ( a / RTV)
Compressibility factor is less than 1.As pressure is increased at constant temperature, V decreases so that the factor a/RTV increases.
3) At high pressure
At high pressure , V is so small that b cannot be neglected in comparison to V. The factor a / V2 is no doubt large but as P is very high, a / V2 can be neglected in comparison to P. Thus van der waals equation reduces to form
P ( V – b ) =RT
PV = RT + Pb
PV/RT = 1 + Pb / RT
Z = 1 + Pb/ RT
Compressibility factor is greater than 1. As pressure is increased , the factor Pb/RT increases. The compressibility factor increases continuously with pressure.
4) At high temperature
At high temperature V is very large, so that both the correction factors become negligible. Hence, at high temperature, real gases behave like real gases.
Exceptional Behaviour of Hydrogen and Helium
For hydrogen and helium, the compressibility factor Z is always greater than 1 and increases with increase of pressure. This is because Hydrogen and helium being . very small, the intermolecular forces of attraction in them are negligible i.e. a is very very small so that a/V2 is negligible.
The Van der waal s equation, therefore become P( V – b ) or PV = RT + Pb
PV/RT = 1 + Pb /RT
Thus PV / RT i.e. Z > 1 and increases with increase in the value of P at constant T.

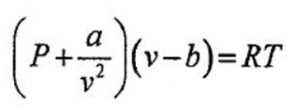
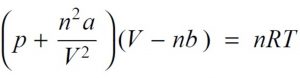
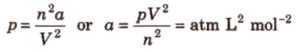
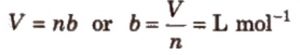
Mrs Shilpi Nagpal you are doing a very good job
your’s content and style of expressing science is very much understandable
Well thank you for clearing my doubts
Ma’am your way of explaning concepts is just incredible.
Thankyou soo much for this content.
Keep up the good work!
your expanation was great and helped a lot please keep doing the noble work.
thank you shilpi maam for this content
Thanks a lot mam..I can’t tell you how much helpful it was..
Its was very help full mam. Thank u mam keep doing this good work. Take care.
Great job have been done by you