Kinetic Molecular Theory Of Gas

Kinetic theory of gases

Postulates or assumptions of kinetic theory of gases

1)Every gas is made up of a large number of extremely small particles called molecules. All the molecules of a particular gas are identical in mass and size and differ in these from gas to gas.

2)The molecules of a gas are separated from each other by large distances so that the actual volume of the molecule is negligible as compared to the total volume of the gas.

3)The distance of separation between the molecules are so large that the forces of attraction or repulsion between them are negligible.

4)The force of gravitation on the molecule is also supposed to be negligible.

5)The molecules are supposed to be moving continuously in different direction with different velocities. Hence they keep on colliding with one another as well as on the walls of the containing vessel.

6)The molecules are supposed to be perfectly elastic hard sphere so that no energy is wasted when the molecules collide with one another or with the walls of the vessel. The energy may however be transferred from some molecules to the other on collision.

7)Since the molecules are moving with different velocities, they possess different Kinetic energies. However ,the average kinetic energy of the molecules of a gas is directly proportional to the Absolute temperature of the gas.

8)The molecules are supposed to be moving continuously in different direction with different velocities. Hence, they keep on colliding with one another as well as on the walls of the containing vessel.

 

Kinetic gas equation

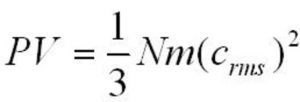
where P= pressure exerted by the gas

V= volume of the gas

m= mass of each molecule of the gas

N= Total number of molecules of the gas present in volume V

c= Root mean square speed of the gas

Kinetic energy and Molecular speeds

In a gas ,the molecules are moving in different directions with different speed colliding with one another as well as the walls of the container. Their individual speeds and hence Kinetic energies keep on changing even at the same temperature. It is found that at a particular temperature, the average kinetic energy of the gas remains constant.

At a particular temperature if n₁ molecules have speed v₁, n₂ molecules have speed v₂ ,n₃ molecules have speed v₃ and so on, then total kinetic energy of the gas at this temperature will be

E_k = ½ m ( n₁v₁² + n₂ v₂² + n₃ v₃²+ …..)

where m is the mass of the molecule of the gas.

Dividing by the total number of molecules, average kinetic energy of the gas will be

½ m( n₁v₁² + n₂ v₂² + n₃ v₃²+ …./ n₁ + n₂ +n₃ )

( n₁v₁² + n₂ v₂² + n₃ v₃²+ …./ n₁ + n₂ +n₃ ) represents the mean of the square of the speeds of different molecules and hence is called mean square speed.Its square root is called root mean square speed.

 

Root mean square speed may be defined as the square root of the mean of the squares of the speed of different molecules of the gas.

c = ( n₁v₁² + n₂ v₂² + n₃ v₃²+ …./ n₁ + n₂ +n₃ )^½

From Kinetic gas equation,

PV= 1/3 mnc²

PV=1/3 Mc²

c= (3PV /M)^½

Putting M/V =d , we get

c= (3P/d )^½

c= ( 3RT/M )^½

Relation between average kinetic energy and absolute temperature

From Kinetic gas equation, we have,

PV = 1/3 mnc²

For 1 mole of a gas, we have

PV = 1/3 Mc²

PV = 2/3 × 1/2 Mc²

But 1/2 Mc² = E_{k ,} total kinetic energy of 1 mole of the gas

Hence, PV = 2/3 E_k

PV = RT for 1 mole of the gas,

RT = 2/3 E_k

Ek = 3/2 RT

Average kinetic energy per molecule ,divide by Avogadro’s number (N_A)

E_{k avg} = 3RT/2N_A

E_{k avg} = 3/2 kT

where k= R/N_A

is called Boltzmann constant = 1.38 × 10^-23 JK^-1

Average Speed

The arithmetic mean of the speeds of different molecules of the gas.If n₁ molecules have speed v₁ , n₂ molecules have speed v₂ ,n₃ molecules have speed v₃ and so on, the average speed will be given by

c _avg = (n₁ v₁ + n₂ v₂ +n₃ v₃ +….) / (n₁ +n₂ +n₃ +…)

c_avg = (8RT / πM )^½