Boyle’s law
The relationship between the volume and pressure of a gas was studied experimentally by Robert Boyle in 1662.
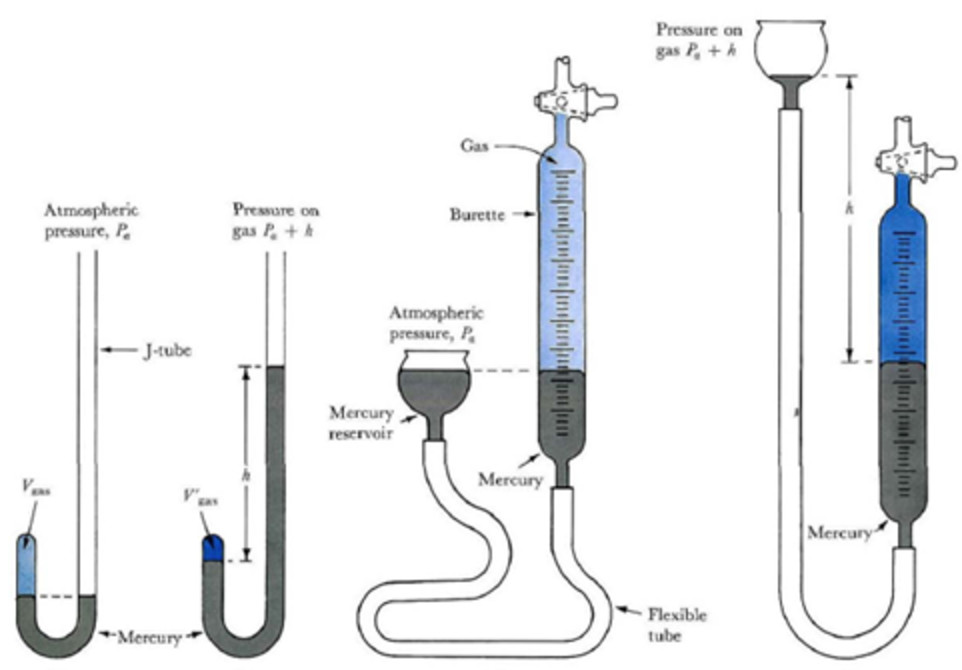
He used mercury and a simple U-tube. The pressure was increased by putting more mercury into the open limb. The volume of the air enclosed in the space above mercury in the shorter limb was noted each time.
Boyle’s law states that
Temperature remaining constant, the volume of a given mass of a gas is inversely proportional to its pressure.
V ∝ 1/P
V =K. 1/P
PV = k
PV=constant at constant temperature
where P and V represents the pressure and volume of the gas and k is a constant whose value depends upon the mass of the gas and the temperature.
The constant value obtained for PV is called Boyle’s constant.
Boyle’s law also states that
Temperature remains constant ,the product of pressure and volume of a given mass of a gas is constant.
If P1 and V1 are the initial pressure and volume of a gas and keeping temperature constant, if pressure is changed to P2, then volume will change to V2 such that according to Boyle’s law,
P1V1 =P2V2 at constant temperature
If the pressure is doubled at constant temperature, the volume is reduced to half. Similarly if pressure is made four times, the volume is reduced to ¼ and so on.
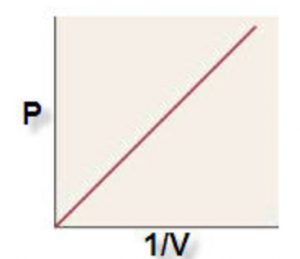
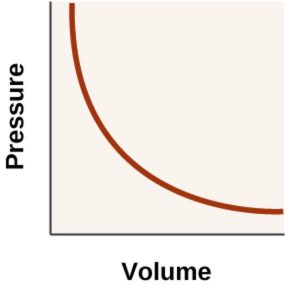
Graphical verification of Boyle’s law
According to Boyle’s law,
P ∝ 1/V
PV = constant
1) P vs 1/V when a straight line passing through the origin is obtained.
2) PV vs P when a straight line parallel to X-axis is obtained.
3) P vs V when branch of hyperbola in the first quadrant is obtained.
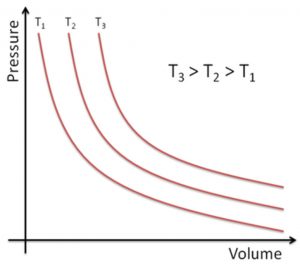
The value of constant depends upon the amount of gas taken and the temperature. Hence, for a given amount of the gas taken, a different temperature P-V curve is obtained at each temperature.
Such P-V curve at constant temperature is called isotherm.
Plots of P vs 1/T obtained at different temperature is:
At constant temperature , for a fixed mass of the gas ,density is directly proportional to pressure.
If m is the mass of gas and V is its volume ,then density d=m/V
By Boyle’s law, PV= k or V= K/P
d= m/(k/P)
d= (m/k)P
d=k’ P
At constant temperature, for a fixed mass of a gas
d ∝P
At altitude ,as the atmospheric pressure is low, the air is less dense. As a result ,less oxygen is available for breathing. The person feels uneasiness and headache. This is called altitude sickness. That is why the mountaineers have to carry oxygen cylinders with them.
Charles law
The effect of temperature on the volume of a gas at constant pressure was first carried out by a French scientist, Jacques Charles in 1787 and then extended by Joseph Gay Lussac in 1802.
Charles law states that
Pressure remaining constant ,the volume of a given mass of a gas increases or decrease by for every 1/273 of its volume for each degree rise or fall in temperature.
Mathematically,
where V is the volume of the gas at t° C and Vo is its volume at 0° C.
At gas at -273° C will have zero or no volume i.e. it will cease to exist.
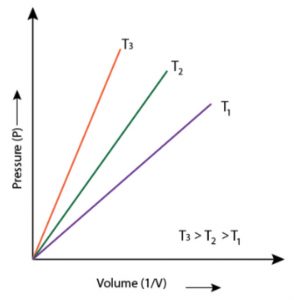
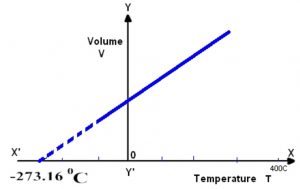
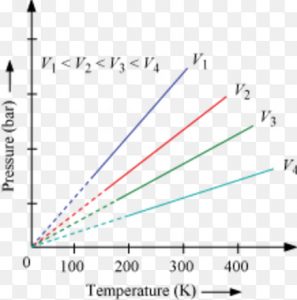
Graphically by plotting the volume of a certain mass of a gas against temperature at constant pressure. We get a graph consisting of a straight line.
If we extrapolate this straight line, it will meet the temperature axis at -273 ° C. At -273° C ,a gas occupies zero or no volume.
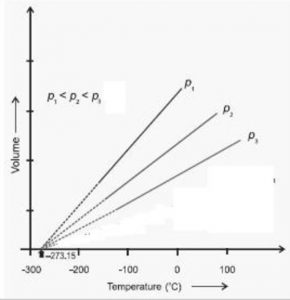
At constant pressure, the straight line V- t plots obtained for different amount of the same gas or for same amount of the different gases are different but each of them intersect the temperature axis at – 273° C corresponding to zero volume.
Each line in the plot is called isobar because it gives a plot of V vs T at constant pressure. Higher the pressure, less, is the slope of the line.
The lowest possible hypothetical or theoretical temperature of -273° C at which gas is supposed to have a zero volume is called absolute zero.
Lord Kelvin has suggested a new scale of temperature starting with – 273° C as its zero. This scale of temperature is known as Kelvin scale or absolute scale. On this scale ,freezing point of water is O° C is 273 °A.
Any temperature on the centigrade scale can be converted to that on the Kelvin scale by just adding to 273 to its value on the centigrade scale.
The two scales are connected by the relation
T K = t ° C + 273
where T and t° C are the temperature on the Kelvin and centigrade scale. This scale of temperature is also called Thermodynamic scale of temperature.
The volume of a gas and its temperature on the Kelvin scale are directly proportional to each other.
According to Charles law,
273 + t = T, the corresponding temperature on the kelvin scale, we get
As Vo and 273 are constant hence,
Vt ∝T
V=kT
The numerical value of k depends upon the amount of the gas taken and the pressure.
Pressure remaining constant ,the volume of a given mass of a gas is directly proportional to its temperature in degree Kelvin.
The relation V ∝ T implies that V/T = constant at constant pressure
If V1 is the volume of a gas at temperature T1 and keeping the pressure constant, temperature is changed to T2 , then volume will change to V2 such that
Air expands on heating and hence its density decreases. Thus hot air is lighter than the atmospheric air. This fact is made use of in filling hot air in the balloons which rise up for metrological observations.
Gay-lussac’s law
It states that
Volume remaining constant, the pressure of a given mass of a gas increases or decreases by 1/273 of its pressure at 0 ° C for every 1 ° C rise or fall in temperature.
where Pt and Po are the pressure of a certain amount of gas at t°C and 0° C.
The numerical value of the constant k depends upon the amount of gas taken and the volume.
Volume remaining constant ,the pressure of a given mass of a gas is directly proportional to its temperature in degree kelvin.
At constant molar volume ,the plot of pressure versus temperature will be a straight line .Such a plot is called isochore.
Avogadro’s Law
Equal volume of all gases under the same conditions of temperature and pressure contain equal number of molecules.
One mole of each gas at the same temperature and pressure should have the same value.
Molar volume of gas under different conditions
When Standard temperature and pressure condition (STP) are taken are 0 °C and 1 atm pressure, molar volume of the gas =22400 ml.
When Standard temperature and pressure condition (STP) are taken are 0 °C and 1 bar pressure, molar volume of the gas =22700 ml.
When Standard temperature and pressure condition (STP) are taken are 25 °C and 1 bar pressure, molar volume of the gas =24800 ml.
According to Avagadro’s Law,
V ∝ n
V=kn
n=m/M
V=k(m/M)
M= k(m/V)
M=kd
The density of a gas is directly proportional to its molar mass.
Combined gas law
The equation which gives the simultaneous effect of pressure and temperature on the volume of a gas is known as ideal gas equation or equation of state.
Let the volume of a certain mass of a gas change from V1 to V2 when the pressure is changed from P1 to P2 and temperature from T1 to T2.
Suppose that the volume of a given mass of a gas changes from V1 to v when the pressure is changed from P1 to P2 at constant T1.
According to Boyle’s Law
P2 × v = P1 × V1
v= (P1 × V1) / P2
Suppose that the volume v changes to V2 when the temperature is changed from T1 to T2 at constant pressure P2.
v / T1 = V2 / T2
V2 = v × (T2 / T1)
V2 = (P1 × V1 × T2 ) / ( P2 × T1)
( P × V ) = constant = K
The value of K depends only upon the amount of the gas taken. If n is the number of moles of the gas taken, then it is found that
K ∝n
K= n R
where R is a constant of proportionality and is found to be independent of the nature of the gas and depends only on the amount of the gas taken.
R is called universal gas constant.
P V = n R T
This is ideal gas equation.
Derivation of Ideal gas equation from laws.
According to Boyle’s law V ∝ 1/P at constant T
According to Charles’s law V ∝ T at constant P
According to Avogadro’s law V ∝ n at constant T and P
V ∝ 1/P × T × n
V= R × (1/P) × T × n
P V = n R T
For 1 mole of the gas, the ideal gas equation becomes
P V = R T
A gas which obeys ideal gas equation is called ideal gas.
If m is the mass of the gas in grams and M is the molecular mass of the gas, then
n = m/ M
P V = n R T
P V = (m / M) R T
P = (m R T) /( V M)
P = (d R T) / M
d= (P M) / (R T)
M = ( d R T )/ (P)
Under similar conditions of temperature and pressure, densities of different gases are directly proportional to their molar masses.
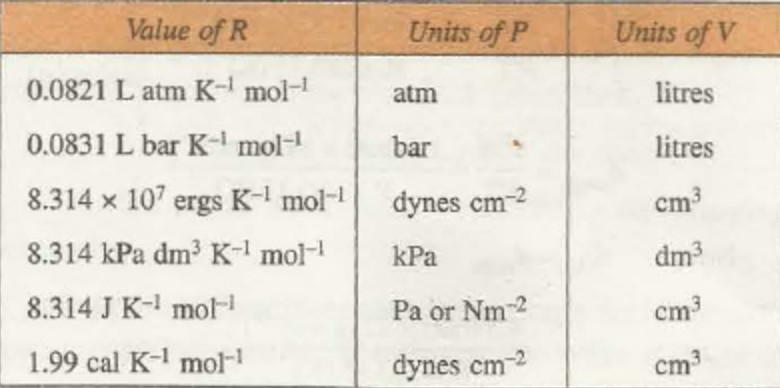
Numerical values of R
1) At N.T.P. condition for 1 mole of a gas
P= 1 atm, V= 22.4 L, T= 273 K, n=1 mole
R = ( P × V ) / ( n × T )
R = 0.0821 litre atm degree-1 mol-1
If V= 224400 cm3 , R = 82.1 cm3 atm degree-1 mol-1
P =1 bar, V= 22.7 dm3 , R= 0.083 bar dm3 K-1 mol-1
2) In C.G.S., units ,for 1 mol of the gas at N.T.P.
P= 76 cm = 76 × 13.6 × 981 dyne/ sq cm
V= 22400 ml , T = 273 K ,n =1 mole
R = 8.314 × 10 7 ergs degree-1 mol-1
3) 107 ergs = Joule
R= 8.314 J K-1 mol-1
P= 101325 N m-2 or Pa
V= 0.0224 m3 ,T= 273 K
R= 8.314 J K-1 mol-1
P= 101.325 kPa , V= 22.4 dm3 , T = 273 k
R = 8.314 kPa dm3 K-1 mol-1
4) In terms of calories,
R = 1.987 calories degree-1 mol-1
Dalton’s Law of Partial Pressure
If two or more chemically non-reactive gases are enclosed in the same vessel, the pressure exerted by the mixture were first studied by John Dalton in 1807.
If two or more gases which do not react chemically are enclosed in a vessel, the total pressure exerted by the gaseous mixture is equal to the sum of all the partial pressure that each gas would exert when present alone in the same vessel at the same temperature.
Partial pressure of a particular gas in a gaseous mixture enclosed in a given space implies the pressure which that gas would exert when present alone in the same space at the same temperature. Let p1, p2,p3…pn be the partial pressure of n gases enclosed in a given vessel and P be the total pressure of the gaseous mixture. Then by Dalton’s law of partial pressure we have
P= p1+ p2+p3+..pn
Application of Dalton’s Law of Partial Pressure
1)In the determination of pressure of a dry gas
Whenever a gas is collected over water, it is moist ,that is ,it is saturated with water vapours which exert their own pressure. The pressure due to water vapour is called aqueous tension.
If P and P’ are the pressure of the moist gas and dry gas at t° C and p is the aqueous tension at that temperature, then by Dalton’s law of partial pressure
P = P’ + p
P’ = P- p
P dry gas = Pmoist gas – Aqueous tension
2)In calculation of partial pressure
In a mixture of non reacting gases A, B, C if each gas is considered to be an ideal gas ,then applying
PV= nRT
we have
PA = ( nA R T ) /V
PB = ( nB R T ) /V
Pc = (nc R T ) /V
Total Pressure P= pA + pB + Pc +………
P = (R T ( nA + nB + nC)) / V
pA / P = nA /( nA + nB + nC)
pA = xA × P
pB = xB × P
pC = xC × P
Partial Pressure of A = Mole fraction × Total pressure
Graham’s law of Diffusion/Effusion
The spreading of the molecules of a gas throughout the available space is called diffusion.
Effusion is a process in which a gas under pressure escapes out of a fine hole in a vessel.
For ex: leaking out of a gas from a cylinder or air from a punctured tyre or escaping out of perfume molecules through the atomizer etc.
Thomas Graham observed that the lighter gases are inversely proportional to the square root of their densities.
For two gases having densities d1 and d2 and rates of diffusion r1 and r2 under similar conditions of temperature and pressure,
The rate of diffusion or effusion
Rate of diffusion / effusion = (Volume of the gas effused or diffused ) / Time taken
Calculation of Molecular masses
Ratio of densities of two gases is equal to ratio of the vapour density.
Molecular mass= 2 × vapour density
If two gases are taken at different pressure ,than as greater the pressure ,greater is the number of molecules hitting per unit area ,greater is the rate of diffusion.
Graham’s law of diffusion can be written as
For two gases undergoing diffusion at the same pressure but at two different temperatures.
r1/ r2 = (T1 M2 / T2 M1 ))½
Comparison of volumes of two different gases effused or diffused in the same time.
Suppose v1 is the volume of gas 1 diffused in time t and v2 is the volume of a gas 2 diffused in the same time t under the same condition of temperature and pressure.
Rate of diffusion (r1) of gas 1 = v1 / t
Rate of diffusion (r2 ) of gas 2 = v2 / t
If d1 and d2 are their densities or M1 and M2 are their respective molecular masses, then
r1 / r2 = (M2 / M1)½
Volumes of two gases effused or diffused in the same time under similar conditions of temperature and pressure are inversely proportional to the square roots of their densities.
Comparison of time taken for effusion or diffusion of same volume of two different gases
Suppose t1 is the time taken for the gas 1 for diffusion of volume v1 and t2 is the time taken for gas 2 for diffusion of the same volume v under same condition of temperature and pressure and through the same orifice.
r1 / r2 = (v / t1) / (v / t2 )
r1 / r2 =( M2 / M1 )½
Time taken for effusion or diffusion of same volume of two different gases under the same conditions of temperature and pressure are directly proportional to the square roots of their densities.
Importance of Graham law of diffusion or effusion
1)It helps in the separation of gases having different densities.
2)It helps in the separation of isotopes of certain elements.
3)It helps to determine the densities or molecular masses of an unknown gas by comparing its rate of diffusion with known gas.

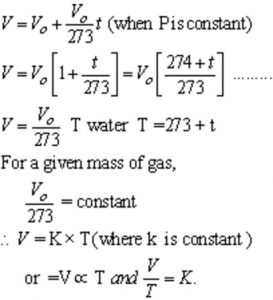
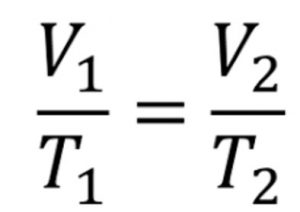

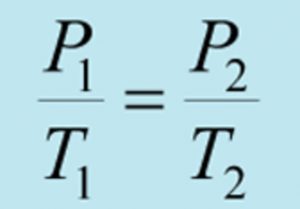


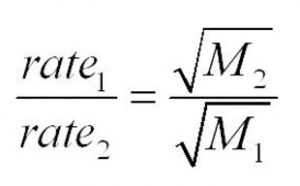
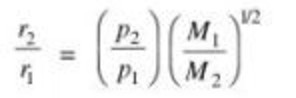
Can you pls mail this chapter ( states of matter )
great explanation thank you so much for lovely notes…….
Was very useful for me!
Thanks ! these notes was really helpful for me because I didn’t got any good notes out there on internet dedicated to just the gaseous laws , THANKS A LOT again
This is a comprehensive note on gas law God bless you Mam.. This alone can make someone pass chemistry class. Thanks