NCERT Answers for Class 6 Maths |
Chapter 14 Practical Geometry Exercise 14.4
Page 284
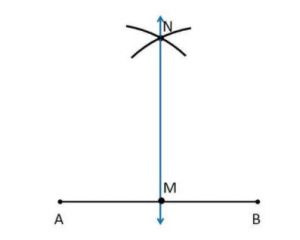
Ex 14.4 Class 6 Maths Question 1. Draw any line segment AB. Mark any point M on it. Through M, draw a perpendicular to AB. (use ruler and compasses)
Answer
Step 1: Draw a line segment AB and mark any point M on it.
Step 2: Place pointer at A as center, and radius more than AM, draw an arc. With B as center, and same radius as before, draw an arc.
Step 3: Mark the point of intersection of the two arcs as point N Join M & N.
MN is the line perpendicular to line AB
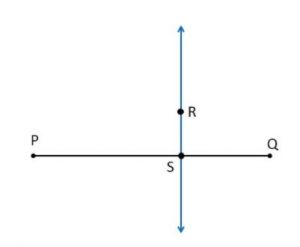
Ex 14.4 Class 6 Maths Question 2. Draw any line segment PQ . Take any point R not on it. Through R, draw a perpendicular to PQ . (use ruler and set-square)
Answer
Step 1: Draw a line segment PQ and a point R outside of PQ
Step 2: Place a set square on PQ such that one side of its right angle be along it.
Step 3: Place a ruler along the longer side of the set square.
Step 4: Hold the ruler fix and slide the set square along the ruler till it touches the point R.
Step 5: Join RS along the edge through R. Thus RS ⊥ PQ.
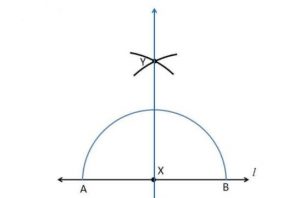
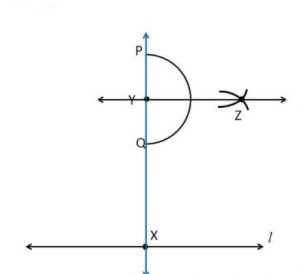
Ex 14.4 Class 6 Maths Question 2. Draw a line l and a point X on it. Through X, draw a line segment XY perpendicular to l. Now draw a perpendicular to XY at Y. (use ruler and compasses)
Answer
Step 1: Draw a line l and take a point X on it.
Step 2: Draw an arc with centre X and of suitable radius to intersect the line l at two points A and B.
Step 3: With P and Q as centres and a radius greater than P draw two arcs to intersect each other at Y.
Step 4: Join YX and produce to Y.
Step 5: With Y as centre and a suitable radius, draw an arc to intersect XY at two points P and Q.
Step 6: With P and Q as centres and a radius greater than YQ , draw two arcs to intersect each other at Z.
Step 7: Join Y and Z. Thus YZ ⊥ XY .
Leave a Reply