NCERT Solutions for Class 7 Maths Chapter 6 The Triangle and its Properties Exercise 6.3

NCERT Solutions for Class 7 Maths
Chapter 6 The Triangle and its Properties
Exercise 6.3

Class 7 Maths Triangle and its Properties Exercise 6.1 Class 7 Maths Triangle and its Properties Exercise 6.2 Class 7 Maths Triangle and its Properties Exercise 6.3

1. Find the value of the unknown x in the following diagrams:

Answer

(i) We know that,
The sum of all the interior angles of a triangle is 180^o.
Then,
= ∠BAC + ∠ABC + ∠BCA = 180^o
= x + 50^o + 60^o = 180^o
= x + 110^o = 180^o
By transposing 110^o from LHS to RHS it becomes – 110^o
= x = 180^o – 110^o
= x = 70^o

(ii) We know that,
The sum of all the interior angles of a triangle is 180^o.
The given triangle is a right angled triangle. So the ∠QPR is 90^o.
Then,
= ∠QPR + ∠PQR + ∠PRQ = 180^o
= 90^o + 30^o + x = 180^o
= 120^o + x = 180^o
By transposing 110^o from LHS to RHS it becomes – 110^o
= x = 180^o – 120^o
= x = 60^o

(iii) We know that,
The sum of all the interior angles of a triangle is 180^o.
Then,
= ∠XYZ + ∠YXZ + ∠XZY = 180^o
= 110^o + 30^o + x = 180^o
= 140^o + x = 180^o
By transposing 140^o from LHS to RHS it becomes – 140^o
= x = 180^o – 140^o
= x = 40^o

(iv) We know that,
The sum of all the interior angles of a triangle is 180^o.
Then,
= 50^o + x + x = 180^o
= 50^o + 2x = 180^o
By transposing 50^o from LHS to RHS it becomes – 50^o
= 2x = 180^o – 50^o
= 2x = 130^o
= x = 130^o/2
= x = 65^o

(v) We know that,
The sum of all the interior angles of a triangle is 180^o.
Then,
= x + x + x = 180^o
= 3x = 180^o
= x = 180^o/3
= x = 60^o
∴ The given triangle is an equiangular triangle.

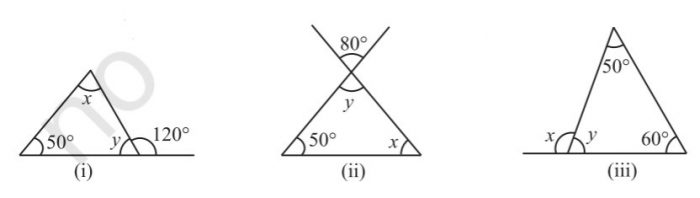
2. Find the values of the unknowns x and y in the following diagrams:

Answer

(i) We Know that, an exterior angle of a triangle is equal to the sum of its interior opposite angles.
Then,
= 50^o + x = 120^o
By transposing 50^o from LHS to RHS it becomes – 50^o
= x = 120^o – 50^o
= x = 70^o
We also know that,
The sum of all the interior angles of a triangle is 180^o.
Then,
= 50^o + x + y = 180^o
= 50^o + 70^o + y = 180^o
= 120^o + y = 180^o
By transposing 120^o from LHS to RHS it becomes – 120^o
= y = 180^o – 120^o
= y = 60^o

(ii) From the rule of vertically opposite angles,
= y = 80^o
Then, we know that,
The sum of all the interior angles of a triangle is 180^o.
Then,
= 50^o + 80^o + x = 180^o
= 130^o + x = 180^o
By transposing 130^o from LHS to RHS it becomes – 130^o
= x = 180^o – 130^o
= x = 50^o

(iii) We know that, the sum of all the interior angles of a triangle is 180^o.
Then,
= 50^o + 60^o + y = 180^o
= 110^o + y = 180^o
By transposing 110^o from LHS to RHS it becomes – 110^o
= y = 180^o – 110^o
= y = 70^o
Now, from the rule of linear pair,
= x + y = 180^o
= x + 70^o = 180^o
By transposing 70^o from LHS to RHS it becomes – 70^o
= x = 180^o – 70
= x = 110^o

(iv) From the rule of vertically opposite angles,
= x = 60^o
Then, we know that, the sum of all the interior angles of a triangle is 180^o.
Then,
= 30^o + x + y = 180^o
= 30^o + 60^o + y = 180^o
= 90^o + y = 180^o
By transposing 90^o from LHS to RHS it becomes – 90^o
= y = 180^o – 90^o
= y = 90^o

(v) From the rule of vertically opposite angles,
= y = 90^o
Then, we know that, the sum of all the interior angles of a triangle is 180^o.
Then,
= x + x + y = 180^o
= 2x + 90^o = 180^o
By transposing 90^o from LHS to RHS it becomes – 90^o
= 2x = 180^o – 90^o
= 2x = 90^o
= x = 90^o/2
= x = 45^o

(vi)
From the rule of vertically opposite angles,
= x = y
Then, we know that, the sum of all the interior angles of a triangle is 180^o.
Then,
= x + x + x = 180^o
= 3x = 180^o
= x = 180^o/3
= x = 60^o