NCERT Solutions for Class 7 Maths
Chapter 6 The Triangle and its Properties
Exercise 6.1
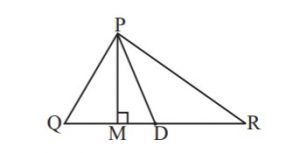
1. In ∆ PQR, D is the mid-point of QR .
PM is _________________.
PD is _________________.
Is QM = MR?
Answer
PM is an altitude from the vertex P to the opposite side QR of ΔPQR. PD is the median from the vertex P to the mid-point of opposite side QR of ΔPQR.
No, QM ≠ MR because M is not the mid-point of QR.
2. Draw rough sketches for the following:
(a) In ∆ABC, BE is a median.
(b) In ∆PQR, PQ and PR are altitudes of the triangle.
(c) In ∆XYZ, YL is an altitude in the exterior of the triangle.
Answer
(a) In the adjoining figure, we have ΔABC. We know that, a median connects a vertex of a triangle to the mid-point of the opposite sides. On joining B and mid-point of BC i.e. E we get the required median BE.
(b) We know that, the perpendicular line segment rom a vertex of a triangle to its opposite de is called an altitude of the triangle. In the adjoining figure, we have ΔPQE in which PQ and PR are the altitude drawn from vertex Q to PR and from vertex R to PQ respectively.
(c) In the adjoining figure, we have an obtuse angled triangle XYZ in which YL is an altitude drawn from Y to produced XZ such altitude lies in the exterior of the triangle.
3. Verify by drawing a diagram if the median and altitude of an isosceles triangle can be same.
Answer
Draw a line segment BC. By paper folding locate the perpendicular bisector of BC. The folded crease meets BC at D, its mid-point.
Take any point A on this perpendicular bisector.
Thus, the triangle obtained is an isosceles ΔABC in which AB= AC.
Since, D is the mid-point of BC, so, AD is its median. Also, AD is perpendicular bisector of BC. So, AD is the altitude of ΔABC.
Thus, it is verified that the median and altituted of an isosceles triangle are same.
Leave a Reply