NCERT Solutions for Class 7 Maths
Chapter 6 The Triangle and its Properties
Exercise 6.2
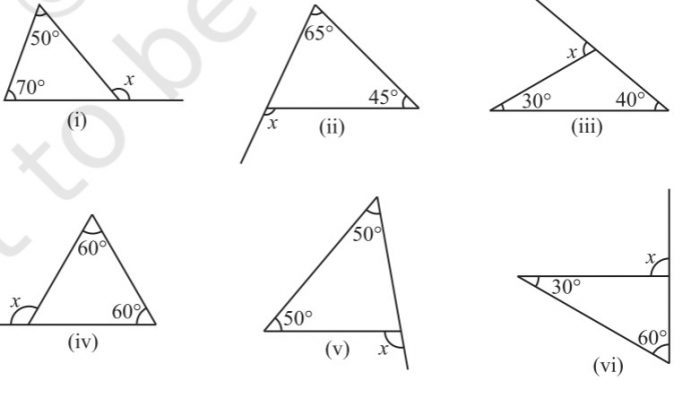
1. Find the value of the unknown exterior angle x in the following diagrams:
Answer
By exterior angle property of a triangle,
Exterior angle = Sum of interior opposite angles
⇒ x=50°+ 70° = 120°
Hence, the exterior angle x is 120°.
(ii) By exterior angle property of a triangle,
Exterior angle = Sum of interior opposite angles
⇒ x= 65°+ 45°= 110°
Hence, the exterior angle x is 110°.
(iii) By exterior angle property of a triangle,
Exterior angle = Sum of interior opposite angles
⇒ x=30° + 40°= 70°
Hence, the exterior angle x is 70°.
(iv) By exterior angle property of a triangle,
Exterior angle = Sum of interior opposite angles
⇒ x= 60° + 60° = 120°
Hence, the exterior angle x is 120°.
(v) By exterior angle property of a triangle,
Exterior angle = Sum of interior opposite angles
∴ x = 50° +50° = 100°
Hence, the exterior angle x is 100°.
(vi) By exterior angle property of a triangle,
Exterior angle = Sum of interior opposite angles
⇒ x = 30°+ 60° = 90°
Hence, the exterior angle x is 90°.
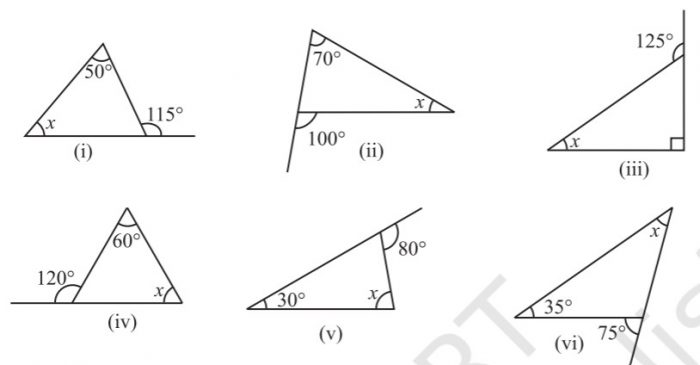
2. Find the value of the unknown interior angle x in the following figures:
Answer
⇒ x = 115° – 50° = 65°
Hence, the value of the unknown interior angle x is 65°.(ii) Sum of interior opposite angles = Exterior angle
⇒ x+ 70° =100°
⇒ x = 100° – 70° = 30°
Hence, the value of the unknown interior angle x is 30°.
(iii) Sum of interior opposite angles = Exterior angle
⇒ x+90° = 125°
⇒ x = 125° – 90°= 35°
Hence, the value of the unknown interior angle x is 35°.
(iv) Sum of interior opposite angles = Exterior angle
⇒ x+60° =120°
⇒ x=120° – 60° = 60°
Hence, the value of the unknown interior angle x is 60°.
(v) Sum of interior opposite angles = Exterior angle
⇒ x+ 30° = 80°
⇒ x= 80° – 30° = 50°
Hence, the value of the unknown interior angle x is 50°.
(vi) Sum of interior opposite angles = Exterior angle
⇒ x+35° = 75°
⇒ x = 75°- 35° = 40°
Hence, the value of the unknown interior angle x is 40°.
Leave a Reply