Vapour Pressure of Liquid Solutions

Vapour Pressure of Liquid

When a liquid is allowed to evaporate in a closed vessel, part of the liquid evaporates and fills the available space with the vapours. Since the vapours leave the container, these get collected in the vapour state above the surface of the liquid.

Due to vaporisation, liquid changes into vapours and level of liquid decreases. As the evaporation proceeds, the number of gaseous molecules in the vapour phase increases gradually.

These molecules move about at random in a limited space during their random movement, some of these strike the surface of liquid and get condensed. The process of condensation acts in opposite direction to the process of evaporation. Thus, both evaporation and condensation processes go on simultaneously.

A stage is reached when the rate of evaporation becomes equal to rate of condensation and an equilibrium gets established between liquid and vapour phases.

The pressure exerted by the vapours above the liquid surface in equilibrium with the liquid at a given temperature is called vapour pressure.

 

Factors on which vapour pressure of a liquid depends

1) Nature of the liquid

Each liquid has a characteristic vapour pressure because each liquid has different magnitude of intermolecular forces.

The liquids, which have weaker intermolecular forces, tend to escape readily into vapour phase and therefore, have greater vapour pressure.

For example: dimethyl ether and alcohol have higher vapour pressure than water at a given temperature because of weaker intermolecular forces in them as compared to water.

2) Temperature

The vapour pressure of a liquid increases with increase in temperature. This is due to the fact that with increase in temperature, more molecules will have larger kinetic energies. Therefore, larger number of molecules will escape from the surface of the liquid to the vapour phase resulting in higher vapour pressure.

(a) Vapour Pressure of Liquid-Liquid Solution

When a binary solution of two volatile liquids is placed in a closed vessel, both the components would evaporate and eventually an equilibrium would be established between vapour phase and the liquid phase.

The French chemist Francois Marte Raoult (1886) gave a quantitative relationship between the partial pressure and the mole fractions of two components. This relationship is known as Raoult’s law which states that

at a given temperature, for a solution of volatile liquids, the partial vapour pressure of each component in solution is equal to the product of the vapour pressure of the pure component and its mole fraction.

Consider a binary solution of two volatile liquids and denote the components as A and B having the mole fraction x_A and x_B . If p_A and p_B are the vapour pressures of the components in the solution, then according to Raoult’s law

p_A =p_A° x_A

p_B =p_B° x_B

where p_A° is the vapour pressure of the pure component A and p_A° is the vapour pressure of pure component B at the same temperature.

 

According to Dalton’s law of partial pressures, the total pressure p over the solution phase in the container will be the sum of the partial pressure of the components of the solution.

This is given as

p=p_A + p_B

Substituting the values of pA and pB we get

p= p_A° x_A + p_B° x_B

x_A + x_B = 1

x_A =1-x_B

p= p_A°(1- x_B) + p_B° x_B

p= p_A° – p_A° x_B  + p_B° x_B

p= p_A° – x_B ( p_B° – p_A° )

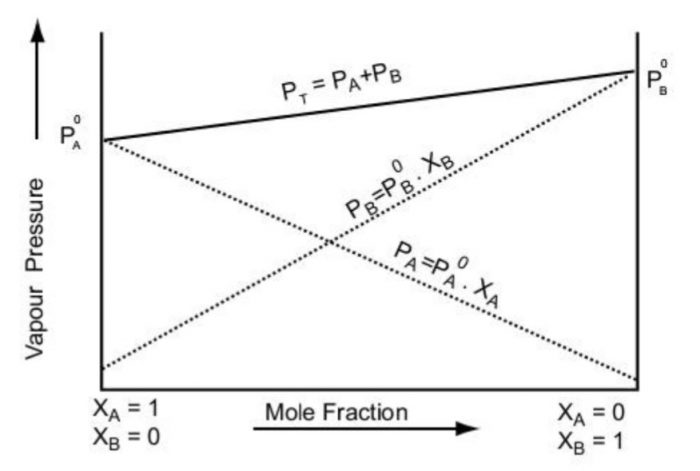
a) Total vapour pressure over the solution can be related to the mole fraction of any one component (x_B or x_A(1-x_B))

b) Total vapour pressure of the solution varies linearly with the mole fraction of component B because p_A° and p_B° are constant.

c) Depending on the vapour pressure of the pure components A and B, total vapour pressure over the solution decreases or increases with the increase of the mole fraction of the component A.

The total vapour pressure (p) is a linear function of the mole fraction x_B (or x_A as x_A =1-x_B ) because p_A° and p_B° are constant at a particular temperature.

The dotted lines give the partial pressure of the two components versus composition and the solid line gives the vapour pressure versus composition.

According to Raoult’s law, the partial vapour pressures of two components A and B of a solution are given as:

p_A = p_A° x_A

p_B = p_B° x_B

Therefore, the vapour pressures of the components are linear functions of their mole fractions. Now

1) when x_A=1, i.e., the liquid is pure A

p_A =p_A° × 1 = p_A°

2) when x_A = 0, i.e., the liquid is pure B

p_A =p_A° × 1 = 0

Thus, the vapour pressure of such solutions is either higher or lower than that predicted by Raoult’s law.

Thus, the plot of p against x_A should give a straight line passing through p_A° (when x_A=1) and 0 (when x_A = 0)

When the liquid is pure (x_A =1), its vapour pressure is equal to p_A°. As component B is  added to component A (x_A decreases), the vapour pressure decreases till it becomes zero (x_A=0)

The variation of partial pressure of component B (p_B) with its mole fraction (x_B) is represented by the plot from x_B =0 (i.e. p_B= p_B° × 0 = 0) to x_B =1 (i.e. p_B=p_B°)

The total vapour pressure p, exerted by the solution as a whole at any composition is given by the sum of partial vapour pressures according to Dalton’s law of partial pressures.

 

Thus

p= pA +pB

p= p_A° x_A  + p_B° x_B

The vapour pressure of solutions of different compositions, lies between the vapour pressure of the pure components (p_A° and p_B°) and they lie on the straight line joining p_A° and p_B°.

The minimum value of p (total vapour pressure) is p_A° and the maximum value is p_B°  assuming that the component A is less volatile than component B i.e p_A° < p_B°

(b) Vapour Pressure of Solution of Solid in Liquid

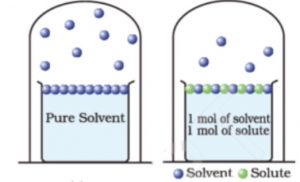
Add a small amount of a non-volatile solute to the solvent (e.g, sugar in water) to form the solution. When evaporation of this solution takes place, the vapour phase again consists of vapours of the solvent (i.e., of water) because the solute is non-volatile.The vapour pressure of the solution is found to be less than that of the pure solvent.

The vapour pressure depends on the escape of solvent molecules from the surface of the liquid.In the case of solution, the non-volatile sugar molecules occupy a certain surface area. As a result lesser number of solvent molecules will escape into vapours. Vapour pressure of the solution will be less than that of the pure solvent or there will be a lowering in vapour pressure. The increase in the concentration of sugar in the solution will further lower the vapour pressure of the solution.

Raoult’s law for liquid solutions containing non-volatile solutes

According to Raoult’s law the partial vapour pressure of volatile component in the solution is directly proportional to the mole fraction in it. When the solute is non-volatile, only the solvent molecules are present in the vapour phase. Therefore, the vapour pressure of the solution will be the vapour pressure due to solvent only.

If P_A is the vapour pressure of the solvent over a solution containing non-volatile solute and x_A is its mole fraction, then according to Raoult’s law, the vapour pressure of the solvent in the solution,

p_A =p_A° x_A

p=p_A°x_A

p(solution) = p(pure solvent) × mole fraction of solvent

This relationship is known as Raoult’s law.

For solutions containing non-volatile solutes, the Raoult’s law may be stated as:

At a given temperature, the vapour pressure of a solution containing non-volatile solute is directly proportional to the mole fraction of the solvent.

If vapour pressure of the solution containing a non volatile solute is plotted against the mole fraction of the solvent, a straight line plot will be obtained as:

Rearranging the above equation, P/ P_A° = x_A

Subtracting each side of the equation from 1, we have

1- (p/p_A°) = 1- x_A

(p_A°- p) / p_A°  = x_B

(p°_solvent -p_solution) /p°_solvent = x_solute

p_A°- p_A(difference in vapour pressure of pure solvent and solution)represents the lowering in vapour pressure on the formation of solution.

Thus, the Raoult’s law in its modified form may be stated as: 

the relative lowering in vapour pressure of an ideal solution containing the non-volatile solute is equal to the mole fraction of the solute at a given temperature.

 

Raoult’s law as a special case of Henry’s law

The vapour pressure of a volatile component in given solution is given by the relation:

p_A =P_A° x_A

where p_A° is the vapour pressure of the pure component, p_A is the vapour pressure in the solution having mole fraction x_A. In the case of solution of a gas in a liquid, the gaseous component is volatile component. Its solubility is governed by Henry law which gives the relation:

p=K_H x

where p is the pressure of the gas above the solution and x is its mole fraction ,K_H  is a proportionality constant known as Henry’s constant.

The partial pressure of the volatile component or gas is directly proportional to its mole fraction in solution. The only difference in the two expressions is the proportionality constant P_A° (in Raoult’s law) and K_H (in Henry’s law). Therefore, Raoult’s law becomes a special case of Henry’s law in which K_H becomes equal to vapour pressure of the pure component (p_A°).