Contents
Solutions
A solution is a homogeneous mixture of two or more substances whose composition can be varied within certain limits.
The substances making up the solution are called components of the solution.
Depending upon the total components present in the solution, it is called the binary solution (two components), ternary solution (three components), quaternary solution (four components), etc.
A component which is present in the largest quantity is called the solvent while the component which is present in lesser quantity is termed the solute.
A solute is a substance that dissolves and a solvent is a substance in which dissolution takes place.
For example: If a crystal of sugar is dropped into a beaker of water, it dissolves to form a solution. In this case, sugar is solute and water is solvent.
Types of solution
Depending upon the physical states of the solute and the solvent, the solutions can be classified into the following types.
Different types of Solutions
| Solute | Solvent | Common Examples |
| Gaseous Solution | ||
| Gas | Gas | Air |
| Liquid | Gas | Water vapours in air |
| Solid | Gas | Dust or smoke particles |
| Liquid Solution | ||
| Gas | Liquid | CO2 dissolved in water |
| Liquid | Liquid | Ethanol dissolved in water |
| Solid | Liquid | Sucrose or salt in water |
| Solid Solutions | ||
| Gas | Solid | Solution of hydrogen in Pd |
| Liquid | Solid | Mercury with sodium(amalgams) |
| Solid | Solid | Copper dissolved in gold (alloys) |
The solutions in which water is the called aqueous solutions while those in which water is not the solvent are called non-aqueous solutions.
For Example: Carbon tetrachloride, benzene, ether etc.
Methods for expressing the concentration of solution
The concentration of a solution may be defined as the amount of solute present in the given quantity of the solution.
The solution is dilute means relatively very small quantity of solute is present or the solution is concentrated means that relatively large quantity of solute is present.
Mass Percentage
The mass percentage of a component in a given solution is the mass of the component per 100 g of the solution.
For example: If WA is the mass of component A and WB is the mass of component B in a solution, then
Mass percentage of A = WA / (WA + WB) × 100
A 10% (w/w) solution of sodium chloride means that 10 g of sodium chloride is present in 90 g of water so that the total mass of the solution is 100 g or simply 10 g of sodium chloride is present in 100 g of solution.
Volume Percentage
The volume percentage is defined as the volume of the component per 100 parts by volume of the solution.
If VA and VB are the volume of two components A and B respectively in a solution, then
Volume percentage of A = VA / (VA + VB) x 100
For example: 10% by volume of ethanol solution means that 10 mL of ethanol is dissolved in enough water so that the the solution is 100 mL. Solutions containing liquids are commonly expressed as volume percentage.
Mass by volume percentage (w/v)
We express the concentrations as weight/volume. It is the mass of solute dissolved in 100 mL of the solution.
For example: A 10% solution of sodium chloride (w/v) means that 10 g of sodium chloride are dissolved in 100 mL of solution.
Parts Per Million
When a solute is present in very minute amounts (trace quantities), the concentration is expressed in parts per million abbreviated as ppm.
It is the parts of a component per million parts of the solution. It is expressed as
For example: Suppose a litre of public supply water contains about 3 x 10-3 g of chlorine.
The mass percentage of chlorine is : (3.0×10-3) / 1000 × 100
= 3 × 10-4
The parts per million parts of chlorine is:
ppm of chlorine = (3.0 x 10-3 x 106) / 1000
= 3
Atmospheric pollution in cities due to harmful gasses is generally expressed in ppm.
Molarity of a solution
It is the number of moles of the solute dissolved per litre of the solution. It is represented as M. Thus, a solution which contains one gram mole of the solution dissolved per litre of the solution is regarded as one molar solution.
For example: 1M Na2CO3 (molar mass = 106) solution has 106 g of the solute present per litre of the solution.
Molarity = (Moles of solute / Volume of solution in litres) × 1000
The units of molarity are moles per litre (mol L-1)
or moles per cubic decimetre (mol dm-3).
The symbol M is used for mol L-1 or mol dm-3
If nB moles of solute are present in V mL of solution, then
Molarity = nB / V x 1000
Moles of solute = Moles of solute / Molar mass of solute
Molarity has one disadvantage. It changes with temperature because of expansion or contraction of the liquid with temperature.
Molality
Molality is considered better for expressing the concentration as compared to molarity because the molarity changes with temperature because of expansion on contraction of the liquid with temperature. However, molality does not change with temperature because mass of the solvent does not change with change in temperature.
It is the number of moles of the solute dissolved per 1000 g (or 1 kg) of the solvent. It is denoted by m.
Thus, a solution which contains one gram mole of a solute dissolved in 1 kg of water is regarded as 1 molal solution.
For example: 1.0 m solution of KCl means that 1 mol (74.5 g) of KCl is dissolved in 1 kg or
1000 g of water.
The units of molality are moles per kilogram i.e., mol kg-1. It is represented by the symbol m.
If nB moles of solute are dissolved in W grams of solvent, then
Molality = nB / V x 100
Mole Fraction
It is the ratio of number of moles of one component to the total number of moles (solute and solvent) present in the solution.
A solution contains nA moles of solute and nB moles of the solvent.Then
The sum of mole fractions of all the components in solution is always equal to one.
If the mole fraction of one component of a binary solution is known, that of the other can be calculated.
XA =1-XB
XB =1- XA
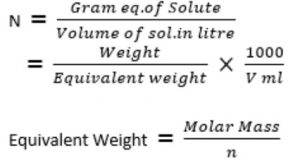
Normality
It is the number of gram equivalents of the solute dissolved per litre of the solution. It is denoted by N.
The units of normality are gm equivalent per litre i.e, g equiv L-1.
Like molarity, normality of a solution also changes with temperature.
Relationship between Normality and Molarity of Solutions
The normality and molarity of a solution are related as:
Normality = (Molarity x Molar mass) / Equivalent mass
For acids,
Normality = Molarity x Basicity
where basicity is the number of H+ ions that a molecule of an acid can give in solution.
For example: Normality of H2SO = 2 x Molarity of H2SO4
Normality of H3PO4 = 3 x Molarity of H3PO4
For bases,
Normality = Molarity x Acidity
where acidity is the number of OH¯ ions that a molecule of base can give in solution.
For example: Normality of KOH = 1 x Molarity of KOH
Normality of Ba(OH)2 = 2 × Molarity of Ba(OH)2
Formality
It is the number of formula masses of the solute dissolved per litre of the solution. It is represented by F.
The term formality is used to express the concentrations of ionic substances.
The ionic compounds such as NaCl, KNO3, CuSO4, etc. do not exist as discrete molecules. In such cases, we do not use the term mole for expressing the concentration. The sum of the atomic masses of various atoms constituting the formula of the ionic compounds is called gram formula mass.
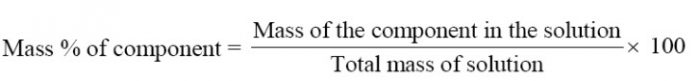
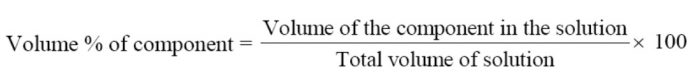
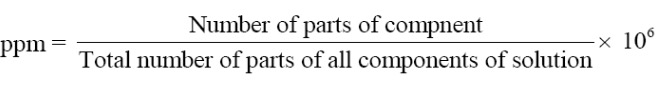
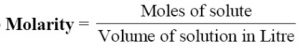
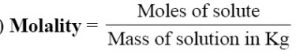
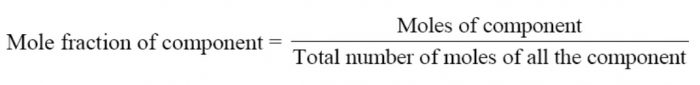
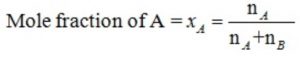
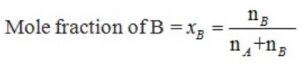


I pray to allah for your kindness
Thank you so much for this brilliant notes, really applicative and helpful one… Lacking words to say!
your notes are excellent madam
awesome notes, thanks
good thoughts i salute you mam