Contents
Abnormal Molecular Masses
The accurate values of molar masses can be obtained only if the following two conditions are met.
(i) The solutions should be dilute
The solutions used for measuring colligative properties must not be too concentrated. In the concentrated solutions, the particles begin to interact with each other as well as with the solvent. As a result, the vapour pressure and therefore, other colligative properties depend upon the nature of the solute and not just on the number of solute particles.
(ii) The solute must not dissociate or associate in solution
The equations derived for measuring the colligative properties are for non-electrolyte solutes which do not undergo any dissociation or association in the solution.
Discrepancies in determination of molar mass arise when the solute dissociate or associate on dissolving in a solvent. This is because due to the association or the dissociation of the solute molecules in the solution, the number of molecules undergo a change.
The discrepancy in molar mass is called abnormal molar mass. The abnormal molar masses is due to association or dissociation of solute particles.
Association of Solute Particles
In certain solvents, generally non-polar, the solute molecules undergo association i.e. two, three or even more molecules exist in combination with each other to form bigger molecules. For example: suppose n simple molecules combine to form an associated molecule as :
nA ⇔ An
Therefore, the total number of molecules in solution become less than the number of molecules of the substance added and, therefore, colligative properties will be lower. Since the colligative properties are inversely proportional to the molar mass of the solute, the molar masses in such cases will be greater than the theoretical values.
For example: In benzene solvent, both ethanoic acid (acetic acid) and benzoic acid exist as dimers as:
2CH3COOH ⇔ (CH3COOH)2
2C6H5COOH ⇔ (C6H5COOH)2
The molar masses of ethanoic acid and benzoic acid have been found to be nearly 120 and 244 which are about double than their normal values of 60 and 122. The association of solute molecules in a solution is generally due to the hydrogen bonding between these molecules.
For example: benzoic acid and ethanoic acid exist as dimers due to the formation of hydrogen bonds. Due to association of ethanoic acid or benzoic acid, the ΔTf or ΔTb value will be about half of the normal value. Therefore, the molar mass calculated on the basis of ΔT will be about twice the expected value.
Dissociation of Solute Molecules
Molecules of certain substances (acids, bases and salts) dissociate or ionise in a solvent to give two or more particles.
For example: AB dissociates to give double number of particles as:
AB ⇔ A+ + B–
The total number of particles increases in solution and, therefore, the colligative properties of such solutions will be large. Since colligative properties are inversely proportional to molar mass, the observed molar mass will be less than the theoretical value.
For example, KCl dissociates to give K+ and Cl– ions.
KCl ⇔ K+ + Cl–
If we dissolve 1 mol of KCl (74.5 g) in water, we expect 1 mol of K+ and 1 mol of Cl– ions to be produced in the solution. Therefore, there would be 2 mol of particles in the solution instead of 1 mol. Consequently, the colligative properties would also be about double than expected.
For example: if we ignore interionic attraction, 1 mol of KCl in 1 kg of water would be expected to increase the boiling point by 2 X 0.52 K (Kb= 0.52 Km-1) = 1.04 K.
Van’t Hoff Factor
In 1886, Van’t Hoff introduced a factor called Van’t Hoff factor, i , to express the extent of association or dissociation of solutes in solution. It is the ratio of the normal and observed molar masses (or abnormal molar mass) of the solute, i.e.
In case of association, observed molar mass being more than the normal, the factor i has a value less than 1.
But in case of dissociation, the Van’t Hoff factor is more than 1 because the observed molar mass has a lesser value.
In case of solutes which do not undergo any association or dissociation in a solvent, the Van’t Hoff factor i will be equal to 1 because the observed and normal molar masses will be same.
Since the molar masses are inversely proportional to the colligative property. Van’t Hoff factor may also be expressed as:
Relative lowering in vapour pressure = i xsolute = Δp / p°
Elevation in boiling point , Δ Tb =i Kb m
Depression in freezing point = Δ Tf = i Kf m
Osmotic pressure π = i cRT
Van’t Hoff Factor and Extent of Dissociation or Association in an Electrolytic Solution
Van’t Hoff factor can be used to calculate the extent of dissociation or association in terms of degree of dissociation or association of a substance in solution.
(i) Degree of dissociation: It is defined as the fraction of total substance that undergoes dissociation into ions, i.e.
Degree of dissociation = No. of moles of the substance dissociated / Total number of moles of the substance taken
Suppose a molecule of an electrolyte gives n ions after dissociation. Then if we start with 1 mole of the solute, and α is the degree of dissociation, then at equilibrium:
Number of moles of solute left undissociated =1-α
Number of moles of ions formed = nα
Total number of moles of particles 1-α+ nα
Van’t Hoff factor, i =
Observed number of moles of solute / Normal number of moles of solute
Knowing the value of i from observed molar mass and normal molar mass, degree of dissociation, α can be calculated.
For the electrolytes of the type AB, such as KCl, NaCl, etc,.the number of particles in solution i.e. n=2
For the electrolytes of the type AB, like CaCl2, Ba(NO3)2 etc, the value of n=2, so that
α = ( i-1 ) /2
(ii) Degree of association: It is defined as the fraction of total number of molecules which combine to form associated molecules, i.e.
|
Degree of association = No. of moles of the substance associated / Total number of moles of substance taken |
For example: suppose n simple molecules of the solute associate to form the associated molecule A.
nA= An
If we start with 1 mole of A and α is the degree of association, the concentration of the species after association is
[An] = α/n
[A] =1-α
Total number of moles after association = 1-α+ α/n
Thus, the colligative properties will correspond to (1-α+ α/n) mole particles rather than one mole of particles.
Van’t Hoff factor, i , is : Observed number of moles of solute / Normal number of moles of solute
= 1-α + α/n / 1
= 1+ α (1/n -1)
α =( i-1 ) /( 1/n -1)
i= Normal molar mass / Observed molar mass
Knowing n the number of simple molecules which combine to give associated molecule, observed molar mass, degree of association(α) can be calculated.

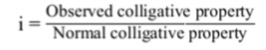
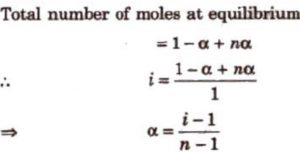
Very good effort me also M.sc hons. M.phil chemistry work as principal.In this lock down period ur notes are helping me a lot
That’s a great work to help out by sharing your experience and passion for needy one. It is really very helpful for the betterment of students in this crucial time period. I’m also M.Sc. (chemistry) & looking for research scholar after lockdown.
I’m working as a PGT-chemistry since 2012. Very nice and generous you are indeed….
This is vey helpful for the students as it is simply written and easily understandable. I’m taking help from here to make my notes. I value your concernity.
Very very nice
It’s really helpful
Fantastic work!!