Electrolytic Conduction

Electrolytic Conduction

When a voltage is applied to the electrodes dipped into an electrolytic solution, ions of the electrolyte move and, therefore, electric current flows through the electrolytic solution.

The power of the electrolytes to conduct electric current is termed conductance or conductivity. Electrolytic solutions also obey Ohm’s law.

Ohm’s Law

This law states that the current flowing through a conductor is directly proportional to the potential difference across it, i.e. 

I ∝ V

 

where I is the current strength (in amperes) and V is the potential difference applied across the conductor (in volts)

I= V/R  or

V=IR

where R is the constant of proportionality and is known as resistance of the conductor. It is expressed in ohms and is represented as Ω. The strength of current flowing through a conductor is directly proportional to the potential difference applied across the conductor and inversely proportional to the resistance of the conductor.

Resistance

It measures the obstruction to the flow of current. The resistance of any conductor is directly proportional to the length (l) and inversely proportional to the area of cross-section (a) so that 

R ∝ l/a or

R=ρ  ( l / a)

where p (Greek, rho) is the constant of proportionality and is called specific resistance or resistivity. The resistance depends upon the nature of the material.

The unit of resistance is ohm (Ω). In terms of SI, base unit is equal to (kgm²/(s³A²)

Resistivity or specific resistance

R= ρ (1/ α)

Now, l=1 cm, a =1 cm², then R= ρ

 

Thus, resistivity is defined as the resistance of a conductor of 1 cm length and having area of cross-section equal to 1 cm².

Resistivity or specific resistance is the resistance between opposite faces of one centimetre cube of the conductor. It is also expressed as resistance when it is 1 m long and its area of cross section is 1 m² i.e., resistance of one metre cube of the conductor

1 Ω m = 100 Ω cm or

1 Ω cm = 0.01 Ω m

The units of resistivity are

ρ = R  ( a / l ) = (ohm cm²⁾ /cm = ohm cm

Its SI units are ohm metre (Ω m). But quite often ohm centimeter (Ω cm) is also used

Conductance

It is a measure of the ease with which current flows through a conductor. It is expressed as G. It is inverse of the resistance, i.e

G = 1 / R

The units of conductance are reciprocal ohm (ohm^-1 ) or mho. Ohm is also abbreviated as Ω so that ohm^-1 may be written as Ω^-1

According to S.I. system, the units of electrical conductance are siemens,

S (i.e. 1S = 1 Ω^-1 )

Conductivity

The inverse of resistivity is called conductivity (or specific conductance). It is represented by the symbol, κ (Greek kappa)

The conductance of a solution of 1 cm length and having 1 sq cm as the area of cross-section. Conductivity is the conductance of one centimetre cube of a solution of an electrolyte.

κ = 1/ ρ

The units of conductivity are 

κ = 1/ ρ

κ = 1/ ohm . cm

κ = ohm^-1 cm^-1

κ = Ω^-1 cm^-1

 

In SI units, l is expressed in m, area of cross-section in m² so that the units of conductivity are S m^-1. The magnitude of conductivity depends upon the nature of the material.

Molar Conductivity or Molar Conductance

Molar conductivity is defined as the conducting power of all the ions produced by dissolving one mole of an electrolyte in solution.

It is denoted by Λ_m (lambda).

Λ_m = κ / M

where M is the molar concentration. If M is in the units of molarity i.e. moles per litre

(mol L^-1), then Λ may be expressed as :

Λ_m = (κ  × 1000 )/ M

Units of Molar Conductance

The units of molar conductance can be derived from the formula,

Λ_m =( κ x1000 ) /M 

The units of κ are S cm ^-1 and units of Λ are

Λ_m = S cm^-1 x ( cm³ / mol L^-1 )

Λ_m = S cm² mol^-1

Equivalent Conductivity

It is defined as the conducting power of all the ions produced by dissolving one gram equivalent of an electrolyte in solution.

It is expressed as Λ_e and is related to specific conductance as

Λ_e = (κ × 1000 ) / C

where C is the concentration in gram equivalent per litre (or normality). The units of equivalent conductivity are ohm cm² (g equiv^-1) as obtained from the formula:

Λ = (κ x 1000) / C

Λ =[ (S cm^-1) × cm³ L^-1 ] / g equiv L^-1

In terms of SI units, the units of equivalent conductivity are S m² equiv^-1 and Λ is expressed as:

Λ = κ /C 

where κ, is in S m^-1 and C is in g equiv m^-3.

1) Measurement of Conductance

The conductance of a solution is reciprocal of the resistance, therefore, the experimental determination of the conductance of a solution involves the measurement of its resistance.

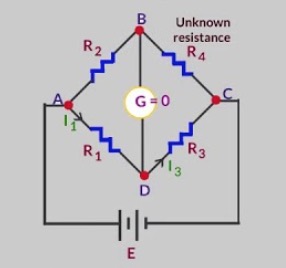
It consists of four arms containing the resistance R₁, R₂, R₃ and R₄. R₂ is the variable resistance and R4 is the unknown resistance. When the current flows through the circuit, the variable resistance is so adjusted to get no current position. This is indicated by no deflection in the galvanometer and is called null point.

 

At null point

R₂/R₄ = R₁ /R₃

Knowing the value of R₁, R₂, R₃ ,unknown resistance R₄ can be calculated.

R₄ = ( R₂ × R₃ ) /  R₁

For measuring the resistance of an ionic solution, we face two difficulties:

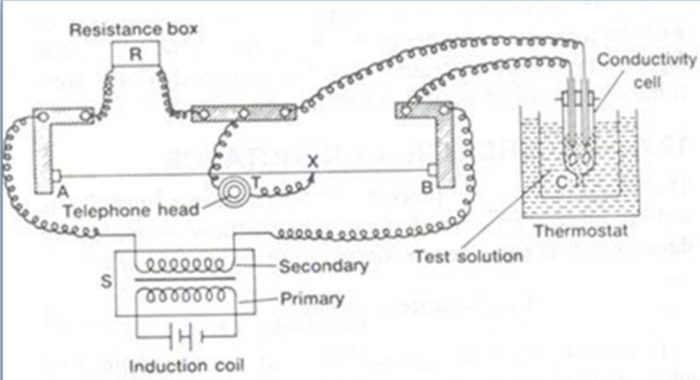
1) For electrolytic solution, direct current cannot be used because it causes electrolysis of the solution.As a result the concentration of the electrolyte changes and this results in the change in the resistance of the solution.To overcome this problem, alternating current in the audio frequency range 550 to 5000 cycles per second is provided by using a suitable electronic circuit commercially available. However, when alternating current is used, ordinary galvanometer fails to detect null point. Since the frequency of alternating current is within the range of human ear, the galvanometer may be replaced by a set of head phones.

2) A solution of unknown resistance cannot be connected to the bridge like a metallic wire or other solid conductor. This problem is solved by using a specially designed vessel called conductivity cell for taking the ionic solution.

The electrodes of the cell are made up of platinum, coated with platinum black. The coating of electrodes with platinum black reduces polarization effects.

 

a) The bridge is connected to a suitable source of alternating current. An alternating current at a frequency 550 to 5000 cycles per second is passed.

b) The solution whose resistance is to be measured (say C) is placed in the conductivity cell and is attached to the wheatstone bridge.

c) The cell is placed in a thermostat to keep the temperature constant.

d) A variable standard resistance box is attached between points.

e) A suitable value of resistance R is taken out from the standard resistance box.

f) The null point is detected by moving the sliding contact on the wire so that minimum sound is obtained in the earphone. This corresponds to null point.

2) Calculation of Conductivity

We have seen that conductivity (κ) is reciprocal of resistivity (ρ), i.e.

κ = 1/ρ

ρ = R (a/l)

κ = ( 1 × l ) /( R × a )

κ = G (l/a)

where G is the conductance of the cell, l is the distance of separation of two electrodes having cross-section area a cm². The quantity (l/a) is called as cell constant and is expressed in cm^-1.

Conductivity = Conductance x Cell constant

3) Determination of Cell Constant 

The cell constant is generally not calculated from the values of l and a because these are difficult to measure for a given cell. However, it is usually determined accurately by measuring the conductance of a standard solution whose conductivity is known. For this purpose, a standard solution of KCl is used whose conductivity is known at different concentrations and temperatures.

Once the cell constant is known, the conductivity of any solution can be easily calculated from the measured resistance or conductance of the electrolytic solution.