Colligative Properties

Colligative Properties

The properties of the solutions which depend only on the number of solute particles but not on the nature of the solute are called Colligative properties.

The four important colligative properties are:

(i) Relative lowering in vapour pressure
(ii) Elevation in boiling point
(iii) Depression in freezing point
(iv) Osmotic pressure.

Relative Lowering in Vapour Pressure

When a non-volatile solute is added to a solvent, the vapour pressure of the solution decreases.

Let x_A be the mole fraction of the solvent, x_B be the mole fraction of the solute and p be the vapour pressure of the pure solvent and p be the vapour pressure of solution.

Since solute in non-volatile, there will be no contribution of solute to the vapour pressure and the vapour pressure of the solution will be only due to the solvent. Therefore, the vapour pressure of the solution (p) will be equal to the vapour pressure of the solvent (p_A), over the solution, i.e.,

p=p_A

But, according to Raoult’s law, the vapour pressure of solvent is equal to the product of its vapour pressure in pure state and its mole fraction, 

p_A =p°_A x_A

p_B = p°_B x_B

 

Since x_A is always less than one, the vapour pressure of the solution is always less than p_A° i.e., vapour pressure of the pure solvent.

The lowering in vapour pressure is

Δp_A = p°_A – p_A

Δp_A = p°_A – p°_A x_A

x_A = 1- x_B

Δp_A = p°_A – p°_A(1- x_B )

Δp_A = p°_A – p°_A + p°_A x_B

Δp_A  = p°_Ax_B

Δp_{A / p°A = xB}

p°_A – p_{A / p°A} = x_B

where, p_A – p°_A (difference in vapour pressure of pure solvent and solution) represents the lowering in vapour pressure on the formation of solution and (p°_A – p_A )/p°_A  gives the relative lowering in vapour pressure. Thus, the relative lowering in vapour pressure of an ideal solution containing the non-volatile solute is equal to the mole fraction of the solute at a given temperature.

Relative lowering of vapour pressure-a colligative property

The relative lowering in vapour pressure depends only on the molar concentration of the solute (mole fraction) and is independent of its nature. Therefore, relative lowering in vapour pressure is a colligative property

Determination of Molar Mass of a Solute from Relative Lowering in Vapour Pressure

A known mass of the solute is dissolved in a known quantity of solution and relative lowering in vapour pressure is measured experimentally.

According to Raoult’s law, the relative lowering in vapour pressure on the addition of a non-volatile solute to the solvent is:

(p°_A – p_A) / p°_{A =  xB}

Suppose w_A and w_B are the weights of the solvent and solute respectively and M_A and M_B are their corresponding molar mass. Then,

Mole fraction of solute =  x_{B / nA+nB}

where n_A and n_B are the moles of the solvent and the solute and

n_A = w_A /M_A

Since the law is applicable to the ideal solutions which are dilute, the molar concentration of the solute being very small can be neglected as compared to that of the solvent. Thus,

 

Thus, the molar mass of the solute can be determined if the other quantities and relative lowering in vapour pressure are known.

Elevation in Boiling Point

The boiling point of a liquid is the temperature at which its vapour pressure becomes equal to the atmospheric pressure.

The vapour pressure of the solution containing non-volatile solute is less than that of the pure solvent. Therefore, the solution has to be heated to a higher temperature  so that its vapour pressure becomes equal to the atmospheric pressure. Thus the boiling point of the solution is always higher than that of the pure solvent.

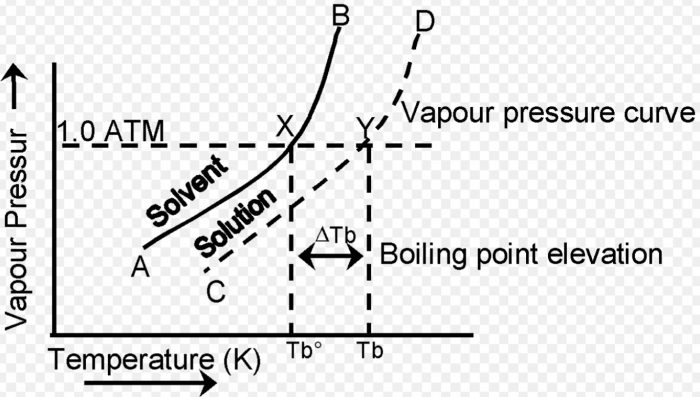
The difference in the boiling points of the solution (T_b) and pure solvent (T_b°) is called the elevation in boiling point (ΔT_b).

The vapour pressure of the pure solvent or solution increases with rise in temperature.

a) The curve AB gives the vapour pressure for the pure solvent and the curve CD gives the vapour pressure for the solution at different temperatures.

b) The curve CD representing the vapour pressure of the solution at different temperatures lies below the curve AB which corresponds to the vapour pressure of the pure solvent. This is because of the fact that the vapour pressure of the solution is less than that of the pure solvent at all temperatures.

c) The vapour pressure of the pure solvent becomes equal to atmospheric pressure at X (corresponding to temperature T_b°) while the vapour pressure of the solution becomes equal to atmospheric pressure at Y (corresponding to temperature T_b).

d) Thus, the b.p. of the pure solvent is T_b° while that of the solution is T_b .Since T_b is greater than T_b° there is an elevation or increase in boiling temperature of the solution as compared to that the solvent.

For example: Vapour pressure of water is 1.013 bar (or 1 atm) at 373 K. Therefore, water boils at 373 K because its vapour pressure at this temperature becomes equal to one atmospheric pressure which is 1.013 bar.The vapour pressure of an aqueous solution of sucrose is less than 1.013 bar at 373 K and therefore, the solution will not boil at 373 K. In order to make the solution to its temperature must be increased so that its vapour pressure becomes equal to 1.013 bar (1 atm).

Mathematically, elevation in boiling point, ΔT_b , may be expressed as :

ΔT_b = T_b – T_b°

 

The elevation in the boiling point (ΔT_b) of a solution is proportional to the molal  concentration of the solution, i.e.,

T_b ∝ m

ΔT_b = K_b m

where m is the molality of the solution and represent moles of solute in 1 kg of solvent and K_b is called molal boiling point elevation constant or molal boiling point constant or ebullioscopic constant.

If m=1

then

ΔT_b = K_b

Thus, molal boiling point elevation constant, K_b is defined as the elevation in boiling point for 1 molal solution i.e. a solution containing 1 gram mole of solute dissolved in 1000 g of the solvent.

Elevation in boiling point-a colligative property

Elevation in boiling point is directly proportional to the molal concentration of the solute (i.e., number of molecules) and therefore, it is a colligative property.

Determination of Molar Mass of Solute from Elevation in Boiling Point Temperature

The elevation in boiling point (ΔT_b) is useful in determining the molar mass of the solute.

Let w_B gram of a non-volatile solute is dissolved in w_A grams of the solvent and M_B is the molar mass of the solute.

Therefore, the molality, m of the solution is:

m = (Moles of solute x 100) / Wt. of solvent in grams

where moles of solute = w_B /M_B

m= (w_B × 1000) / M_B × w_A

ΔT_b = K_b m

ΔT_b = (K_b × w_B × 1000) / M_B × w_A

Thus , molar mass of solute

M_B = (K_b × w_B × 1000) / ΔT_b × w_A

Depression In Freezing point 

At the freezing point of a solvent, the solid and the liquids are in equilibrium. This is only possible if they have the same vapour pressure.

Therefore, a solution will freeze when its vapour pressure becomes equal to the vapour pressure of the pure solid solvent.

Thus, the freezing point is the temperature at which the solid and the liquid states of the substance have the same vapour pressure. When a non-volatile solute is added to a solvent, the freezing point of the solution is always lower than that of the pure solvent.

 

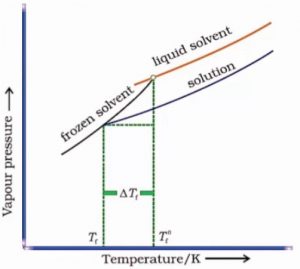
The orange curve gives vapour pressure of the pure solvent. The addition of a non-volatile solute lowers the vapour pressure and the purple curve gives the vapour pressure curve for the solution at different temperature.

The temperature corresponding to the point where the solid and liquid solvent meet (i.e., solid and liquid states have the same vapour pressure) represents the freezing point temperature of pure solvent (T_f°).

The temperature corresponding to the point where the solid solvent and liquid solution meet (i.e., solid and liquid states have the same vapour pressure) represents the freezing point temperature of the solution (T_f)

Since T_f, is less than T_f°, this shows that the freezing temperature of the solution is less than that of pure solvent and the depression in freezing temperature (ΔT_f) is given as:

ΔT_f = T_f°- T_f

The depression in freezing point of a solution is proportional to the molal concentration of the solution i.e.,

ΔT_f  ∝ m

ΔT_f  =K_f  m

where K_f is the molal freezing point depression constant. It is also called molal cryoscopic constant.

If m=1

ΔT_f  =K_f

Thus, molal freezing point depression constant is defined as the depression in freezing point for 1 molal solution i.e, a solution containing 1 gram mole of solute dissolved in 1000 g of solvent.

Depression in freezing point- a colligative property

ΔT_f  ∝ m

The depression in freezing point temperature is directly proportional to the molal concentration of the solute (i.e., number of molecules) and therefore, it is a colligative property

Determination of Molar mass of solute from Depression in Freezing point temperature

The depression in freezing point temperature (ΔT_f) is useful in determining the molar mass of the solute (M_B).

Let wt. of the solute = w_B g

Wt. of solvent = w_A g

Molar mass of the solute = M_B

Molality of solution, m = (w_B × 1000) /(M_B × w_A)

By substituting the value of m in the relation , ΔT_f  = K_f × m

ΔT_f  =( K_f × w_B × 1000 ) / M_B × w_A

M_B  = ( K_f × w_B × 1000 ) / ΔT_f  × w_A