Contents
Experimental Determination of Order of a Reaction
(1) Graphical method
This method is used when there is only one reactant. It involves the following steps:
1) The concentrations of the reactants are measured by some suitable method.
2) A graph is plotted between concentration and time.
3) The instantaneous rates of the reaction at different times are calculated by finding out the slopes of the tangents corresponding to different times.
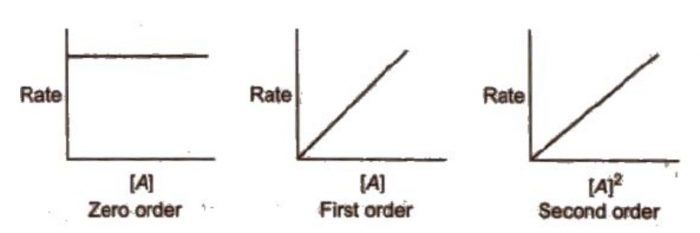
4) The rate of reaction is plotted versus concentration,[A] or (concentration)2, [A]2 and so on.
(a) If rate of reaction remains constant in rate versus concentration graph, it means that the rate is independent of the concentration of the reactant, i.e.
Rate = k [A]0 = k
Therefore, the reaction is of zero order.
(b) If a straight line is obtained in rate versus concentration graph, it means that the rate is directly proportional to concentration of the reactant i.e.
Rate = k [A]
Therefore, the reaction is of first order.
(c) If a straight line is obtained in rate versus (concentration)2 graph, it means that
Rate = k [A]2
Therefore, the order of the reaction is two.
(d) Similarly, if we get straight line in rate versus (concentration)3 graph, then
Rate = k[A]3
and the order of reaction is 3
If we get straight line by plotting graph of rate versus (concentration)n, where n =1, 2, 3…. so on, then
Rate = k[A]n
and the order of reaction is n.
Example : Decomposition of nitrogen pentoxide.
2N205(g) ——-> 4NO2(g) + O2(g)
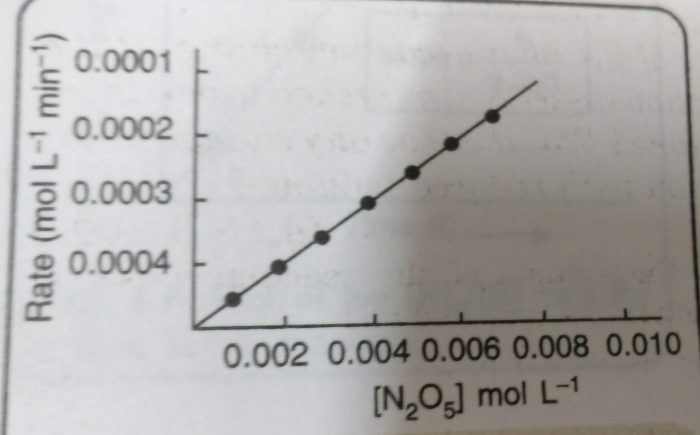
This reaction involves the gaseous reactants and products. Therefore, the reaction can be easily studied by measuring the increase in pressure of the gaseous mixture at different intervals of time. From the measured values of total pressure, the partial pressure of N2O5 at different times can be calculated.
From this, the concentration of N2O5 in moles per litre can be calculated. The molar concentrations of N2O5 obtained are plotted against time. The rates at different times are obtained by measuring the slopes of the tangents corresponding to these times.
Rate = k [N2O5]n
| [N2O5] (mol L-1) | Rate (mol L-1 min) |
| 1.13 × 10-2 | 3.4 × 10-4 |
| 0.84 × 10-2 | 2.5 × 10-4 |
| 0.62 × 10-2 | 1.1 × 10-4 |
| 0.46 × 10-2 | 1.3 × 10-4 |
| 0.35 × 10-2 | 1.0 × 10-4 |
| 0.26 × 10-2 | 0.8 × 10-4 |
The plot of rate versus [N2O5] is a straight line.This means that the rate of the reaction is directly proportional to the [N2O5]. Therefore, the rate law is:
Rate = k [N2O5]
However, we do not get straight line by plotting rate of reaction against [N2O5]2. This means that the reaction is not of second order.
Rate = -dx/dt = k [N2O5]
and order of the reaction is 1.
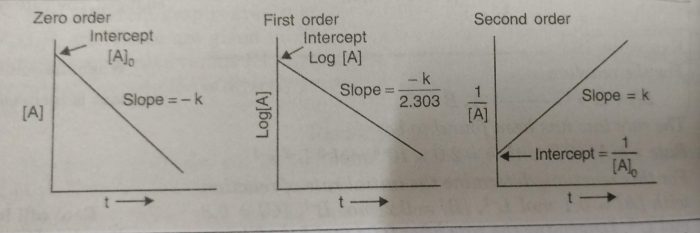
(2) Use of integrated rate equation
The kinetic data is fitted to different integrated rate equation. Wherever the data fit with the equation for the correct order of the reaction, it will give constant value of rate constant for all data points (concentrations at different times).
For a general reaction:
A ———> Products
the integrated rate equation for zero, first and second order reactions are below given:
The straight lines are obtained for a plot of [A] versus t for a zero order reaction.
(3) Initial Rate Method
The graphical methods cannot be applied for the reaction which involve more than one reactant.The rates of such reactions can be determined by initial rate method.
a) The initial rate of the reaction i.e. the rate at the beginning of the reaction is measured.The rate over an initial time interval that is short enough so that concentration of the reactants do not change appreciably from their initial values.This corresponds to slope of the tangent to the concentration versus time graph at t=0.
b) The initial concentration of only one reactant is changed and the rate is determined again.From this order with respect to that particular reactant is calculated.
c) The procedure is repeated with respect to each reactant until the overall rate law is fully determined.
d) The sum of the individual orders with respect to each reactant gives the order of the reaction.
Consider a reaction
aA + bB + c C ——-> Products
The general form of the rate law may be written as :
Rate = k[A]p [B]q [C]r
Then initial rate of the reaction may be given as :
r0 = Rate = k [A]0p [B]oq [C]or
If [B] and [C] are kept constant, then
ro= ko[A]op where ko= k [B]oq [C]or
The value of p can be determined by inspecting the rate at different values of [A].If we know the initial rates at two different concentration of A.
(r0)1=ko[Ao]1p
(r0)2 = ko [Ao]2p
where (r0)1 and (r0)2 are initial rate of reactions when the initial concentration of A are [Ao]1 and [Ao]2
n= p+ q+ c
2A + 2B ———> products
Rate = k[A]p[B]q
(Rate)0= k [A]op[B]oq
(4) Ostwald Isolation Method
The total order of the reaction is then equal to the sum of the orders of reaction for individual reactants.This method is based on the principle that if the concentration of all but one reactant are taken in excess , then during the course of the reaction, the concentration of those reactants taken in excess will remain almost constant and hence variation in rate will correspond to the concentration of that reactant whose concentration is small.This process is repeated one by one and order with respect to each reactant is determined.
The overall order will be the sum of all these orders.
aA + bB + c C ———> Products
Suppose we isolate A by taking B and C in large excess and get order of reaction with respect to A.Similarly , we isolate B by taking A and C in B and and C.
Overall order of reaction n= p+ q+ r

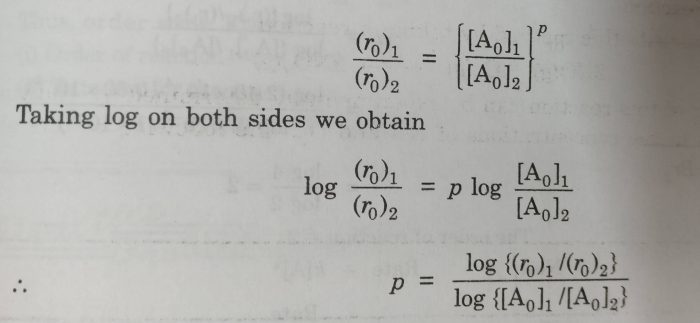
complement of the season,
you’ve been a helping hand to me, God bless you and keep it up. HAPPY NEW YEAR
Thanks
This was really helpful.