Equation of Motion by Graphical Method

Question 1 What is meant by uniform circular motion?

Question 2 A body goes around the sun with constant speed in a circular orbit. Is the motion uniform or accelerated?

Question 3 A satellite goes around the earth in a circular orbit with constant speed. Is the motion uniform or accelerated?

Question 4 Give examples of circular motion?

Question 5 What is a centripetal force. Give example?

Question 6 A cyclist goes around a circular track once every 5 minute. If the radius of the circular track is 110 meters, calculate his speed?

Question 7 Derive first equation of motion by graphical method?

Question 8 Derive second equation of motion by graphical method?

Question 9 Derive third equation of motion by graphical method?

Uniform Circular Motion

When a body moves in a circle, it is called circular motion.

When a body moves along a circular path, then its direction of motion keeps on changing continuously.

Since the velocity changes (due to continuous change in direction) therefore the motion along a circular path is said to be accelerated. When a body moves in a circular path with uniform speed its motion is called uniform circular motion. The velocity of the body moving in a circle with uniform speed is not uniform because the direction of motion is constantly changing.

For Example:

A stone tied to a thread is rotated in circular path with uniform speed in clockwise direction.

A → Speed is directed towards east.
B → Speed is directed towards south.

Since there is change in direction of speed, the velocity is not uniform.
The motion in a circle with constant speed is an example of accelerated motion.
The force which is needed to make an object travel in circular path is called centripetal force.

For Example :

(1) Movement of artificial satellite around earth .
(2) Motion of moon around earth.
(3) Motion of earth around sun.
(4) Tip of seconds hand of a watch.
(5) Athlete moving on a circular path.

The speed of a body moving along a circular path is given by:

                                      v=2nr/t

Equation of Motion by Graphical Method

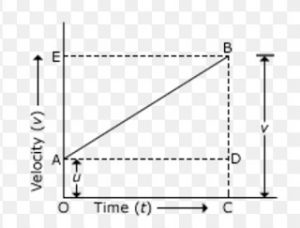
(1) Derivation of v=u + at

Initial velocity u at A =OA
Velocity changes from A To B in time t(uniform acceleration a)
Final Velocity v=BC
BC=BD+DC
v=BD+AO
v=BD+u
Slope of velocity time graph is equal to acceleration a.
a= BD
a=BD/AD
a=BD/t
BD = at
v=u+at     

(2) Derivation of  S = ut +1/2 x at²

The distance travelled by the body is given by area of the space between velocity time graph AB and time axis OC , which is equal to area of figure OABC.
Distance travelled=Area of figure OABC
= Area of rectangle OADC + Area of triangle ABD
=(OA x OC) + 1/2 x AD x BD)
=(u x t) + (1/2 x t x at)
S = ut + 1/2 x at²            

(3) Derivation of v²  = u²  + 2as

The distance travelled by body in time t is given by area of figure OABC (which is a trapezium)

s = Area of trapezium OABC
s= Sum of parallel sides x height / 2
s= (OA+OB) x OC / 2
s=(u+v) x t /2
v=u + at
at = v – u
t= v-u /a
s= (u+v) x (v- u)/2a
2as = v²  – u² 
v²  = u²  + 2as