Exercise 7.3

Exercise 7.1 Exercise 7.2 Exercise 7.3 Exercise 7.4 Exercise 7.5 Exercise 7.6

NCERT Solutions for Class 6 Maths
Chapter 7 Fractions Exercise 7.3

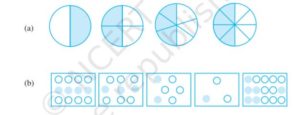
Ex 7.3 Class 6 Maths Question 1. Write the fractions. Are all these fractions equivalent?

Answer :

(a) (i) Shaded part = 1/2

(ii) Shaded part = 2/4 = 1/2

(iii) Shaded part =3/6 = 1/2

(iv) Shaded part = 4/8 = 1/2

Hence, all fractions are equivalent.

(b) (i) Shaded part =4/12= 1/3

(ii) Shaded part = 3/9 = 1/3

(iii) Shaded part =2/6 = 1/3

(iv) Shaded part = 1/3

(iv) Shaded part = 6/15 = 2/5

All the fractions in their simplest form are not equal, hence, they are not equivalent fractions

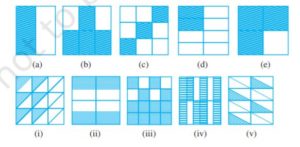
Ex 7.3 Class 6 Maths Question 2. Write the fractions and pair up the equivalent fractions from each row.

Answer:

Ex 7.3 Class 6 Maths Question 3. Replace ☐ in each of the following by the correct number:

(a) 2 / 7 = 8 / ☐

(b) 5 / 8 = 10 / ☐

(c) 3 / 5 = ☐ / 20

(d) 45 / 60 = 15 / ☐

(e) 18 / 24 = ☐ / 4

Answer :

(a) Given

2 / 7 = 8 / ☐

2 × ☐ = 7 × 8

☐ = (7 × 8) / 2

= 28

(b) Given

5 / 8 = 10 / ☐

☐ = (8 × 10) / 5

= 16

(c) Given

3 / 5 = ☐ / 20

☐ = (3 × 20) / 5

= 12

(d) Given

45 / 60 = 15 / ☐

☐ = (15 × 60) / 45

= 20

(e) Given

18 / 24 = ☐ / 4

☐ = (18 × 4) / 24

= 3

Ex 7.3 Class 6 Maths Question 4. Find the equivalent fraction of 3/5 having

(a) denominator 20     (b) numerator 9
(c) denominator 30     (d) numerator 27

(a) We require denominator 20

Let M be the numerator of the fractions

Therefore M / 20 = 3 / 5

5 × M = 20 × 3

M = (20 × 3) / 5

= 12

Therefore the required fraction is 12 / 20

(b) We require numerator 9

Let N be the denominator of the fractions

Therefore 9 / N = 3 / 5

3 × N = 9 × 5

N = (9 × 5) / 3

= 15

Therefore the required fraction is 9 / 15

(c) We require denominator 30

Let D be the numerator of the fraction

Therefore D / 30 = 3 / 5

5 × D = 3 × 30

D = (3 × 30) / 5

= 18

Therefore the required fraction is 18 / 30

(d) We require numerator 27

Let N be the denominator of the fraction

Therefore 27 / N = 3 / 5

3 × N = 5 × 27

N = (5 × 27) / 3

= 45

Therefore the required fraction is 27 / 45

Ex 7.3 Class 6 Maths Question 5. Find the equivalent fraction of 36 / 48 with

(a) numerator 9

(b) denominator 4

Answer:

(a) Given numerator = 9

Therefore 9 / D = 36 / 48

D × 36 = 9 × 48

D = (9 × 48) / 36

D = 12

Hence, the equivalent fraction is 9 / 12

(b) Given, denominator = 4

Therefore N / 4 = 36 / 48

N × 48 = 4 × 36

N = (4 × 36) / 48

= 3

Hence, the equivalent fraction is 3 / 4

Ex 7.3 Class 6 Maths Question 6. Check whether the given fractions are equivalent:

(a) 5 / 9, 30 / 54

(b) 3 / 10, 12 / 50

(c) 7 / 13, 5 / 11

Answer:

(a) Given 5 / 9 and 30 / 54

We have 5 × 54 = 270

9 × 30 = 270

5 × 54 = 9 × 30

Hence, 5 / 9 and 30 / 54 are equivalent fractions

(b) Given 3 / 10 and 12 / 50

We have 3 × 50 = 150

10 × 12 = 120

3 × 50 ≠ 10 × 12

Hence, 3 / 10 and 12 / 50 are not equivalent fractions

(c) Given 7 / 13 and 5 / 11

We have 7 × 11 = 77

5 × 13 = 65

7 × 11 ≠ 5 × 13

Hence, 7 / 13 and 5 / 11 are not equivalent fractions

Ex 7.3 Class 6 Maths Question 7. Reduce the following fractions to simplest form:

(a) 48 / 60

(b) 150 / 60

(c) 84 / 98

(d) 12 / 52

(e) 7 / 28

Answer:

(a)48 / 60 = (12 × 4) / (12 × 5)

= 4 / 5

(b) 150 / 60 = (30 × 5) / (30 × 2)

= 5 / 2

(c) 84 / 98 = (14 × 6) / (14 × 7)

= 6 / 7

(d) 12 / 52 = (3 × 4) / (13 × 4)

= 3 / 13

(e) 7 / 28 = 7 / (7 × 4)

= 1 / 4

Ex 7.3 Class 6 Maths Question 8. Ramesh had 20 pencils, Sheelu had 50 pencils and Jamaal had 80 pencils. After 4 months, Ramesh used up 10 pencils, Sheelu used up 25 pencils and Jamaal used up 40 pencils. What fraction did each use up? Check if each has used up an equal fraction of her/his pencils?

Answer:

Total number of pencils Ramesh had = 20

Number of pencils used by Ramesh = 10

Therefore Fraction = 10 / 20 = 1 / 2

Total number of pencils Sheelu had = 50

Number of pencils used by Sheelu = 25

Therefore Fraction = 25 / 50 = 1 / 2

Total number of pencils Jamaal had = 80

Number of pencils used by Jamaal = 40

Therefore Fraction = 40 / 80 = 1 / 2

Yes, each has used up an equal fraction of pencils i.e 1 / 2

Ex 7.3 Class 6 Maths Question 9. Match the equivalent fractions and write two more for each.

(i) 250 / 400 (a) 2 / 3

(ii) 180 / 200 (b) 2 / 5

(iii) 660 / 990 (c) 1 / 2

(iv) 180 / 360 (d) 5 / 8

(v) 220 / 550 (e) 9 / 10

Answer:

(i) 250 / 400

= (5 × 50) / (8 × 50)

= 5 / 8

25 / 40 and 30 / 48 are two more fractions

(ii) 180 / 200

= (9 × 20) / (10 × 20)

= 9 / 10

18 / 20 and 27 / 30 are two more fractions

(iii) 660 / 990

= (2 × 330) / (3 × 330)

= 2 / 3

20 / 30 and 200 / 300 are two more fractions

(iv) 180 / 360

= (1 × 180) / (2 × 180)

= 1 / 2

20 / 40 and 30 / 60 are two more fractions

(v) 220 / 550

= (2 × 110) / (5 × 110)

= 2 / 5

20 / 50 and 40 / 100 are two more fractions

Therefore The equivalent fractions are

(i) 250 / 100 = (d) 5 / 8

(ii) 180 / 200 = (e) 9 / 10

(iii) 660 / 990 = (a) 2 / 3

(iv) 180 / 360 = (c) 1 / 2

(v) 220 / 550 = (b) 2 / 5