| Exercise 7.1 Exercise 7.2 Exercise 7.3 Exercise 7.4 Exercise 7.5 Exercise 7.6 |
NCERT Answers for Class 6 Maths Chapter 7 Fractions Ex 7.4
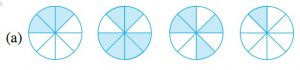
Ex 7.4 Class 6 Maths Question 1. Write shaded portion as fraction. Arrange them in ascending and descending order using correct sign ‘<’, ‘=’, ‘>’ between the fractions:
Answer First circle shows 3 shaded parts out of 8 equal parts. Hence, the fraction is 3 / 8
Second circle shows 6 shaded parts out of 8 equal parts. Hence, the fraction is 6 / 8
Third circle shows 4 shaded parts out of 8 equal parts. Hence, the fraction is 4 / 8
Fourth circle shows 1 shaded parts out of 8 equal parts. Hence, the fraction is 1 / 8
The arranged fractions are:
1 / 8 < 3 / 8 < 4 / 8 < 6 / 8
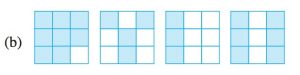
Answer
First square shows 8 shaded parts out of 9 equal parts. Hence, the fraction is 8 / 9
Second square shows 4 shaded parts out of 9 equal parts. Hence, the fraction is 4 / 9
Third square shows 3 shaded parts out of 9 equal parts. Hence, the fraction is 3 / 9
Fourth square shows 6 shaded parts out of 9 equal parts. Hence, the fraction is 6 / 9
The arranged fractions are:
3 / 9 < 4 / 9 < 6 / 9 < 8 / 9
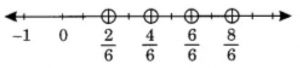
(c) Show 2 / 6, 4 / 6, 8 / 6 and 6 / 6 on the number line. Put appropriate signs between the fractions given.
5 / 6 ☐ 2 / 6, 3 / 6 ☐ 0, 1 / 6 ☐ 6 / 6, 8 / 6 ☐ 5 / 6
Answer Each unit length should be divided into 6 equal parts to represent the fractions 2 / 6, 4 / 6, 8 / 6 and 6 / 6 on number line. These fractions can be represented as follows:
5 / 6 > 2 / 6
3 / 6 > 0
1 / 6 < 6 / 6
8 / 6 > 5 / 6
Ex 7.4 Class 6 Maths Question 2. Compare the fractions and put an appropriate sign.
(a) 3 / 6 ☐ 5 / 6
(b) 1 / 7 ☐ 1 / 4
(c) 4 / 5 ☐ 5 / 5
(d) 3 / 5 ☐ 3 / 7
Answer
(a) Here both fractions have same denominators. So, the fraction with greater numerator is the highest factor
Therefore 3 / 6 < 5 / 6
(b) Multiply by 4
1 / 7 = (1 × 4) / (7 × 4)
= 4 / 28
Multiply by 7
1 / 4 = (1 × 7) / (4 × 7)
= 7 / 28
Here 4 < 7
Therefore 1 / 7 < 1 / 4
(c) Here both fractions have same denominators. So, the fraction with greater numerator is the highest factor
Therefore 4 / 5 < 5 / 5
(d) Here both numerators are same. So, the fraction having less denominator will be the highest factor
Therefore 3 / 7 < 3 / 5
Ex 7.4 Class 6 Maths Question 3. Make five more such pairs and put appropriate signs.
(i) 5 / 8 < 6 / 8
Here, the denominators are same. So, the fraction having greater numerator is the highest factor
(ii) 5 / 8 > 2 / 8
Here, the denominators are same. So, the fraction having greater numerator is the highest factor
(iii) 6 / 13 > 6 / 18
Here, the numerators are same. So, the fraction having lesser denominator will be the highest factor
(iv) 5 / 25 > 3 / 25
Here, the denominators are same. So, the fraction having greater numerator is the highest factor
(v) 9 / 50 < 9 / 45
Here, the numerators are same. So, the fraction having lesser denominator will be the highest factor
Ex 7.4 Class 6 Maths Question 4. Look at the figures and write ‘<’ or ‘>’, ‘=’ between the given pairs of fractions.

(a) 1 / 6 ☐ 1 / 3
(b) 3 / 4 ☐ 2 / 6
(c) 2 / 3 ☐ 2 / 4
(d) 6 / 6 ☐ 3 / 3
(e) 5 / 6 ☐ 5 / 5
Answer
(a) Here, the numerators are same. So, the fraction having lesser denominator is the greater
Therefore 1 / 6 < 1 / 3
(b) 3 / 4 = (3 × 3) / (4 × 3)
= 9 / 12
2 / 6 = (2 × 2) / (6 × 2)
= 4 / 12
Between 4 / 12, 9 / 12
Both fractions have same denominators. So, the fraction having greater numerator will be the greater
Therefore 9 / 12 > 4 / 12
3 / 4 > 2 / 6
(c) Here, the numerators are same. So, the fraction having lesser denominator is the greater
Therefore 2 / 3 > 2 / 4
(d) We get 6 / 6 = 1 and 3 / 3 = 1
So, 6 / 6 = 3 / 3
(e) Here, the numerators are same. So, the fraction having lesser denominator is the greater
Therefore 5 / 6 < 5 / 5
Ex 7.4 Class 6 Maths Question 5. How quickly can you do this? Fill appropriate sign. ( ‘<’, ‘=’, ‘>’)
(a) 1 / 2 ☐ 1 / 5
(b) 2 / 4 ☐ 3 / 6
(c) 3 / 5 ☐ 2 / 3
(d) 3 / 4 ☐ 2 / 8
(e) 3 / 5 ☐ 6 / 5
(f) 7 / 9 ☐ 3 / 9
(g) 1 / 4 ☐ 2 / 8
(h) 6 / 10 ☐ 4 / 5
(i) 3 / 4 ☐ 7 / 8
(j) 6 / 10 ☐ 3 / 5
(k) 5 / 7 ☐ 15 / 21
Answer
(a) Here, the numerators are same. So, the fraction having lesser denominator is the greater
Therefore 1 / 2 > 1 / 5
(b) 2 / 4 = 1 / 2 and 3 / 6 = 1 / 2
Therefore 2 / 4 = 3 / 6
(c) 3 / 5 = (3 × 3) / (5 × 3)
= 9 / 15
2 / 3 = (2 × 5) / 3 × 5)
= 10 / 15
Here, between 9 / 15 and 10 / 15 both have same denominators. Hence, the fraction having greater numerator will be the greater.
Therefore 3 / 5 < 2 / 3
(d) Here, 2 / 8 = 1 / 4
As, 3 / 4 and 1 / 4 have same denominators. Hence, the fraction having greater numerator will be the greater
Therefore 3 / 4 > 2 / 8
(e) Here, the denominators are same. So, the fraction having greater numerator will be the greater
Therefore 3 / 5 < 6 / 5
(f) Here, the denominators are same. So, the fraction having greater numerator will be the greater
Therefore 7 / 9 > 3 / 9
(g) We know 2 / 8 = 1 / 4
Hence, 1 / 4 = 2 / 8
(h) 6 / 10 = (3 × 2) / (5 × 2)
= 3 / 5
Between 3 / 5 and 4 / 5
Both have same denominators. So, the fraction having greater numerator will be greater
Therefore 6 / 10 < 4 / 5
(i) 3 / 4 = (3 × 2) / (4 × 2)
= 6 / 8
Between 6 / 8 and 7 / 8
Both have same denominators. So, the fraction having greater numerator will be greater
Therefore 3 / 4 < 7 / 8
(j) 6 / 10 = (3 × 2) / (5 × 2)
= 3 / 5
Therefore 6 / 10 = 3 / 5
(k) 5 / 7 = (5 × 3) / (7 × 3)
= 15 / 21
Therefore 5 / 7 = 15 / 21
Ex 7.4 Class 6 Maths Question 6. The following fractions represent just three different numbers. Separate them into three groups of equivalent fractions, by changing each one to its simplest form.
(a) 2 / 12 (b) 3 / 15 (c) 8 / 50 (d) 16 / 100 (e) 10 / 60 (f) 15 / 75
(g) 12 / 60 (h) 16 / 96 (i) 12 / 75 (j) 12 / 72 (k) 3 / 18 (l) 4 / 25
Answer (a) 2 / 12 = (1 × 2) / (6 × 2)
= 1 / 6
(b) 3 / 15 = (1 × 3) / (5 × 3)
= 1 / 5
(c) 8 / 50 = (4 × 2) / (25 × 2)
= 4 / 25
(d) 16 / 100 = (4 × 4) / (25 × 4)
= 4 / 25
(e) 10 / 60 = (1 × 10) / (6 × 10)
= 1 / 6
(f) 15 / 75 = (1 × 15) / (5 × 15)
= 1 / 5
(g) 12 / 60 = (1 × 12) / (5 × 12)
= 1 / 5
(h) 16 / 96
= (1 × 16) / (6 × 16)
= 1 / 6
(i) 12 / 75 = (4 × 3) / (25 × 3)
= 4 / 25
(j) 12 / 72 = (1 × 12) / 6 × 12)
= 1 / 6
(k) 3 / 18 = (1 × 3) / (6 × 3)
= 1 / 6
(l) 4 / 25
Totally there are 3 groups of equivalent fractions.
1 / 6 = (a), (e), (h), (j), (k)
1 / 5 = (b), (f), (g)
4 / 25 = (d), (i), (l)
Ex 7.4 Class 6 Maths Question 7. Find answers to the following. Write and indicate how you solved them.
(a) Is 5 / 9 equal to 4 / 5
(b) Is 9 / 16 equal to 5 / 9
(c) Is 4 /5 equal to 16 / 20
(d) Is 1 / 15 equal to 4 / 30
Answer
(a) 5 / 9, 4 / 5
Convert these fractions into like fractions
5 / 9 = (5 / 9) × (5 / 5)
= 25 / 45
4 / 5 = (4 / 5) × (9 / 9)
= 36 / 45
Therefore 25 / 45 ≠ 36 / 45
Hence, 5 / 9 is not equal to 4 / 5
(b) 9 / 16, 5 / 9
Convert into like fractions
9 / 16 = (9 / 16) × (9 / 9)
= 81 / 144
5 / 9 = (5 / 9) × (16 / 16)
= 80 / 144
Therefore 81 / 144 ≠ 80 / 144
Hence, 9 / 16 is not equal to 5 / 9
(c) 4 / 5, 16 / 20
16 / 20 = (4 × 4) / (5 × 4)
= 4 / 5
Therefore 4 / 5 = 16 / 20
Hence, 4 / 5 is equal to 16 / 20
(d) 1 / 15, 4 / 30
4 / 30 = (2 × 2) / (15 × 2)
= 2 / 15
Therefore 1 / 15 ≠ 4 / 30
Hence, 1 / 15 is not equal to 4 / 30
Ex 7.4 Class 6 Maths Question 8. Ila read 25 pages of a book containing 100 pages. Lalita read 2 / 5 of the same book. Who read less?
Answer
Total number of pages a book has = 100 pages
Lalita read = 2 / 5 × 100 = 40 pages
Ila read = 25 pages
Therefore Ila read less than Lalita.
Ex 7.4 Class 6 Maths Question 9. Rafiq exercised for 3 / 6 of an hour, while Rohit exercised for 3 / 4 of an hour. Who exercised for a longer time?
Answer
Rafiq exercised = 3 / 6 of an hour
Rohit exercised = 3 / 4 of a hour
3 / 6, 3 / 4
Convert these into like fractions
3 / 6 = (3 × 2) / (6 × 2)
= 6 / 12
3 / 4 = (3 × 3) / (4 × 3)
= 9 / 12
Clearly, 9 / 12 > 6 / 12
Therefore 3 / 4 > 3 / 6
Therefore Rohit exercised for a longer time than Rafiq.
Ex 7.4 Class 6 Maths Question 10. In a class A of 25 students, 20 passed with 60% or more marks; in another class B of 30 students, 24 passed with 60% or more marks. In which class was a greater fraction of students getting with 60% or more marks?
Answer
Total number of students in Class A = 25
Students passed in first class in Class A = 20
Hence, fraction = 20 / 25
= 4 / 5
Total number of students in Class B = 30
Students passed in first class in Class B = 24
Hence, fraction = 24 / 30
= 4 / 5
Therefore An equal fraction of students passed in first class in both the classes
Leave a Reply