Class 6 Mathematics Chapter 4 |
Basic Geometrical Ideas | Exercise 4.1
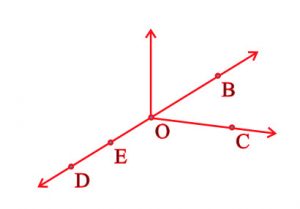
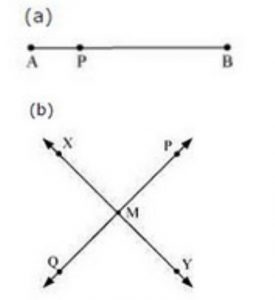
Question 1: Use the figure to name:
(a) Five points
(b) A line
(c) Four rays
(d) Five line segments
Answer 1:
(a) Five points are: O, B, C, D, E
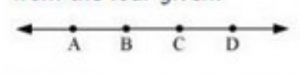
Question 2: Name the line given in all possible (twelve) ways, choosing only two letters at a time from the four given.
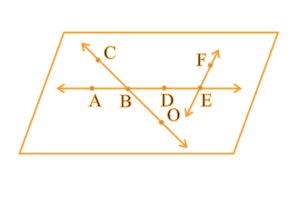
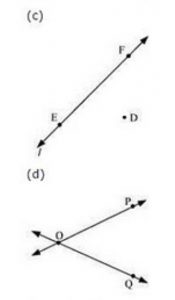
Question 3: Use the figure to name:
(a) Line containing point E.
(b) Line passing through A.
(c) Line on which O lies.
(d) Two pairs of intersecting lines.
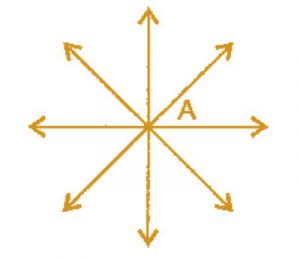
Question 4: How many lines can pass though:
(a) one given point?
(b) two given points
Answer 4: (a) Infinite number of lines can pass through one given point.
(b) Only one line can pass through two given points.
Question 5: Draw a rough figure and label suitably in each of the following cases:
Answer:
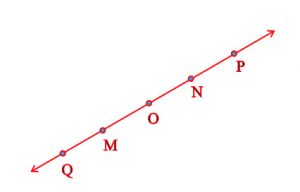
Question 6: Consider the following figure of line MN . Say whether following statements are true or false in the context of the given figure:
Answer 6: (a) True (b) True (c) True (d) False (e) False (f) False (g) True (h) False (i) False (j) False (k) True





Leave a Reply