Contents
Stability Of Coordination compounds in Solution
The stability of a complex in solution means the degree of association between the metal ion and the ligands involved in the state of equilibrium.
The magnitude of the (stability or formation) equilibrium constant for the association express quantitatively the stability.
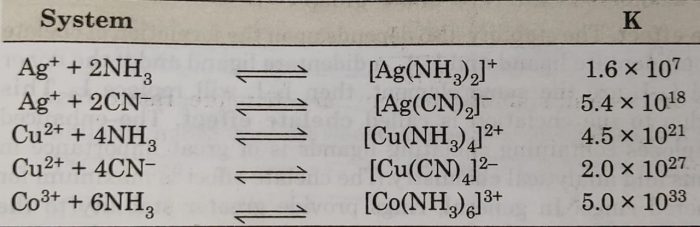
For example: The formation of [Cu(NH3)4]2+ complex may be expressed as :
Cu2+ (aq) +4NH3 (aq) ⇔ [Cu(NH3)4]2+ (aq)
The equilibrium constant for the reaction, is therefore, called the stability constant and is represented by Ks as
The interaction between metal ion and ligand may be regarded as Lewis acid-base reaction. If the interaction is strong, the complex formed would be thermodynamically more stable and the value of stability constant (Ks) will be large.
The larger the numerical value of Ks, the more thermodynamically stable is the complex.
Let us consider a general reaction:
M+4L ⇔ ML4
The stability constant may be written as:
Larger the stability constant, the higher the proportion of ML4 that exists in solution. Since free metal ions rarely exist in the solution so that metal ion (M) will usually be surrounded by solvent molecules which will complete with the ligand molecules, L and be successively represented as :
[M(H2O)n] + 4L ⇔ [ML4] +nH2O
The above overall reaction proceeds in steps with formation constant K1, K2, K3 and K4, for each step as represented below:
where K1, K2, K3 and K4 are called stepwise stability constants
Alternatively, we may write the overall stability constant as
M+ 4L ⇔ ML4
β4 = [ML4] /[M] [L]4
The stepwise and overall stability constants are therefore, related as:
β4 = K1 x K2 x K3 x K4
βn = K1 x K2 x K3 x K4……………..Kn
For example: The steps involved in the formation of the complex ion, tetraamminecopper(III) ion, we have the following:
β4 =[Cu(NH3)4]2+/[Cu2+][NH3]4
Then, logβ may be used as a measure of stability of the complex.
For example:For [Cu(NH3)4]2+, the four constants are :
log β4 = logK1 + logK2 + logK3 + logK4
= 4.0 + 3.2 +2.7 + 2.0
log β4= 11.9
For example: for [Cd(NH3)4]2+
log β4 = 2.6 +2.1 + 1.4 + 0.9 = 7.0
Thus, the log β4 value of [Cu(NH3)4]2+ and [Cd(NH3)4]2+ complexes indicate that [Cd(NH3)4]2+ is more stable than [Cd(NH3)4]2+ complex.
In the second group of qualitative analysis of basic radicals, Cu2+ does not form precipitate as CuS when H2S is passed through the solution containing [Cd(NH3)4]2+ complex, while Cd2+ ions form precipitate as CdS because of instability of [Cd(NH3)4]2+ complex ion.
The reciprocal of stability constant gives the instability constant or dissociation constant of coordination compound, Thus,
Dissociation constant of complex = 1 / Stability constant
The overall stability constant, βn is related to thermodynamic stability when the system has reached equilibrium. Most of the measurements are made from aqueous solutions, which means that the complex is formed by the ligand displacing water molecules from the aqua complex of the metal ion.
Ni2+ + 6 NH3 → [Ni(NH3)6]2+ K= 6.1 × 108
The K values indicate that the bidentate ligand NH2CH2CH2NH2 forms a considerably more stable complex than ammonia.
Factors affecting the stability of a complex ion
(1) The nature of the central ion
The greater the charge and the smaller the size of an ion, i.e., (the larger the charge/radius ratio of an ion), the greater is the stability of its complex. Fe3+ ion carries higher charge than Fe2+ ion but their size is about the same.
Hence charge density is higher on Fe3+ than on Fe2+ ion. The complexes of Fe3+ ion are, therefore more stable.
(ii) Size of metal ion: As the size of the metal ion decreases, the stability of the complex increases. If we consider the bivalent metal ions, than the stability of their complexes (irrespective of the ligands) increases with increase in the ionic radius of the central metal ion as:
| Ion | Mn2+ | Fe2+ | Co2+ | Ni2+ | Cu2+ | Zn2+ |
| Ionic Radius | 91 | 83 | 82 | 78 | 69 | 64 |
Therefore, the order of stability is
This order is called Irving William’s order of stability.
(iii) Electronegativity or charge distribution of metal ion: The stability of complex ion is also related to the electron charge distribution on the metalion.
Metal ions may be classified into two types:
(a) Class ‘a’ acceptors: These are fairly electropositive metals and include the metals of groups 1 and 2, inner transition metals and the early members of the transition series (groups 3 to 6) which have relatively a few electrons beyond an inert gas core. These form most stable coordination entities with ligands containing N, O or F donor atoms.
(b) Class ‘b’ acceptors: These are much less electropositive and include heavy metals such as Rh, Pd, Ag, Ir, Pt, Au, Hg, Pb, etc. having relatively full d-orbitals. These form most stable complexes with ligands whose donor atoms are the heavier members of the N, O and F groups.
(iv) Chelate effect: The stability also depends upon the formation of chelate rings. If L is an unidentate ligand and L-L, a bidentate ligand and if the donor atoms of L and L-L are the same element, then L-L will replace L.
(v) Macrocyclic effect:If a multidentate ligand is cyclic and there are no unfavourable stearic effects, the complexes formed are more stable than corresponding complexes without cyclic ligands. This is called macrocyclic effect.
(2) The nature of the ligand
(ii) Size and charge of ligands: For anionic ligands, the higher the charge and the smaller the size, the more stable is the complex formed. Thus, F¯ ion gives more stable complexes than does Cl¯ ion.
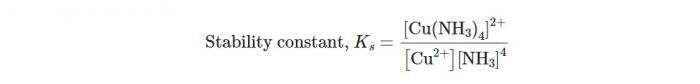
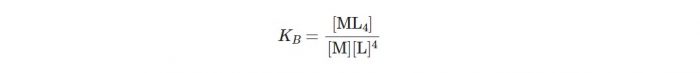

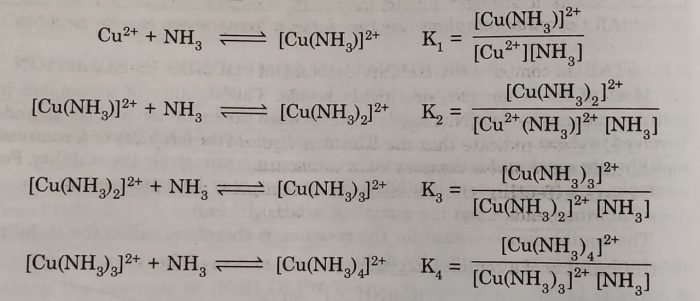
The notes are very clear and precise there easy to understand thanks