Contents
Crystal Field Theory
In negative ligands (anions such as Cl‾, Br‾, CN‾), the interactions with metal ions are ion-ion interactions.
If the ligands are neutral molecules (such as NH3, H2O, CO), the interactions with the metal ions are ion-dipole interactions. For example: In the case of complex ion [CoF6]3- the interactions are between Co3+ and F‾ ions whereas in [Co(NH3)6]3+ the interactions are between negatively charged end of NH3 molecules (δ- charge on N atom) and Co3+ ion.
In free metal ion, all the five d-orbitals have the same energy. These orbitals having the same energies are called degenerate orbitals. This means that an electron can occupy any one of these five d-orbitals with equal ease. On the approach of the ligands, the orbital electrons will be repelled by the lone pairs (or negative charges) of the ligands. The repulsion will raise the energy of the d-orbitals. If all the ligands approaching the central metal ion are at equal distance from each of the d-orbitals, the energy of each orbital will increase by the same amount, due to spherical field or symmetrical field of ligands.
Therefore, these orbitals will still remain degenerate, but they will have higher energy than that of the free ion. d-orbitals have different orientations and, therefore, these orbitals will experience different interactions from the ligands.
The orbitals lying in the direction of the ligands, will experience greater repulsion and their energies will be raised relative to their positions in a symmetrical field.
The orbitals lying away from the approach of the ligands will have lesser interactions with
This conversion of five degenerate d-orbitals of the metal ion into different sets of orbitals having different energies in the presence of electrical field of ligands is called crystal field splitting.
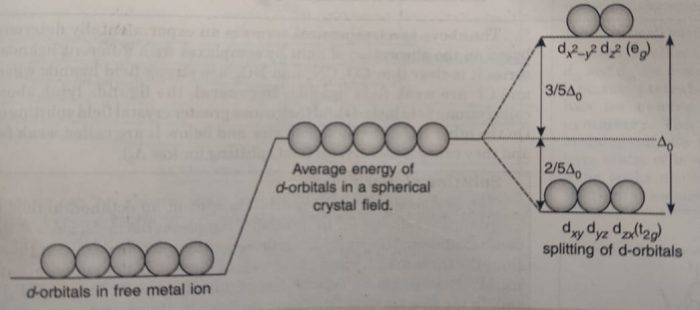
Thus, in coordination compounds, the interaction between the ligand and the metal ion causes the five d-orbitals to split up. The number of ligands (coordination number) and their arrangement (geometry) around the central metal ion will have different effect on the relative energies of the five d-orbitals.
The crystal field splitting will be different in different structures with different coordination numbers.
For example: In case of octahedral complexes, the five d-orbitals split up into two sets; one set consisting of two orbitals dx2-y2 and dz2 of higher energy and another set consisting of three orbitals (dxy, dyz and dzx) of lower energy.
The energy difference between the two sets of energy levels is called crystal field splitting energy and is represented as Δ° (the subscript ‘o’ stands for octahedral).
It measures the crystal field strength of the ligands.
The crystal field splitting occurs in such a way that the average energy of the d-orbitals does not change. This is known as barycentre rule. This means that the three orbitals lie at an energy that is 2/5Δ° below the average d-orbital energy and the two d-orbitals lie at an energy 3 /5 Δ° above the average energy.
Spectrochemical Series
The crystal field splitting ( Δ°) depends upon the nature of the ligands. The greater the ease with which the ligand can approach the metal ion, the greater will be the crystal field splitting caused by it. The ligands which cause only a small degree of crystal field splitting are called weak field ligands while those which cause a large splitting are called strong field ligands.
The ligands can be arranged according to the magnitude of the Δ° and this arrangement is called spectrochemical series. The spectrochemical series in the increasing order of crystal field splitting is given below :
I¯ < Br¯ < SCN¯ < Cl¯ < S2¯ < NO3¯ < F¯ < OH¯ < ox2- < O2– < H2O < NCS¯ < edta 4- < py ≈ NH3 < en < dipy < o-phen < NO2 < CN¯ < CO
The spectrochemical series is an experimentally determined series based on the absorption of light by complexes with different ligands.
(a) CO, CN‾ and NO2‾ are strong field ligands whereas I¯, Br¯ and Cl¯ are weak field ligands.
(b) In the ligands lying above H2O are called strong field ligands and they cause greater crystal field splitting (or high Δ°).
Electronic Structure and Properties of complexes According to C.F.T.
According to Hund’s rule electrons occupy a set of orbitals of same energy one at a time with their spins parallel. The electrons only pair up after each orbital gets one electron. So, for complexes having upto three d-electrons (d1, d2 and d3) each electron can occupy a separate orbital in the lower set.
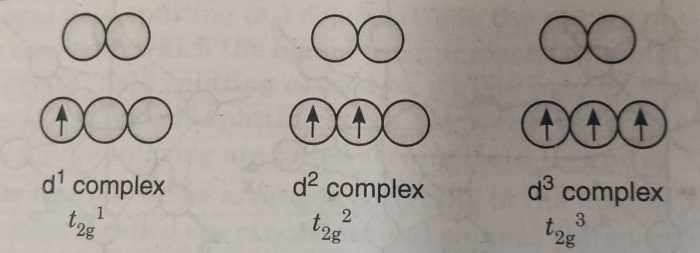
For a d4 complex, there are two possibilities : (a) All the four electrons may occupy lower set of orbitals with one electrons gets paired i.e. t2g4 It experiences a strong repulsion from the electron already there.
(b) The three electrons occupy lower set of orbitals and the fourth electron goes to one of the higher set of orbitals i.e. t2g3 eg1.
Which electronic configuration is possible or has the lower energy depends upon the relative magnitude of the crystal field splitting ( Δ°) and the pairing energy, P (P represents the energy required for electron pairing in a single orbital).
(b) If Δ° is small (as it is for weak field ligands) , then after filling the lower set of three orbitals with one electron each, the next electron goes to the higher set of orbitals. In this case, the repulsion due to pairing of electrons will be more than Δ° . The pairing of electrons will occur only after all the five orbitals are singly filled. In this case, the complex will have maximum number of unpaired electrons and is called high spin complex.
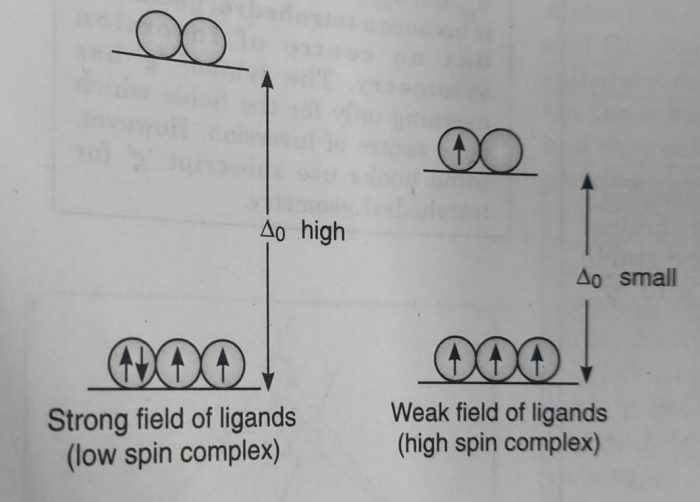
The actual configuration adopted by the complex is decided by the relative values of Δ° and P where P represents the energy required for electron pairing in a single orbital.
(a) If Δ° is less than P (Δ° < P), we have weak field, the fourth electron will enter one of the eg orbitals giving the configuration, t2g3 eg1. It will be high spin complex.
(b) If Δ° is more than P(Δ° > P), we have strong field and the pairing will occur in the t2g orbitals with eg orbitals remaining unoccupied giving the configuration t2g4. It will be low spin complex.
Thus, we can easily predict whether an octahedral complex is likely to be high spin or low spin complex by noting the position of the ligands in the spectrochemical series.
Strong Field Ligand form = Low spin complex
(1) The complexes of Fe (III) such as [Fe(CN)6]3- and [Fe(H2O)6]3+
Fe3+ has 3d5 electronic configuration having five electrons. Now, CN¯ is a strong field ligand and we expect large splitting of d-orbitals. As a result, the five d-electrons will try to remain in lower set and will pair up. This results in low spin complex which will have only one unpaired electron.
H2O is a weak field ligand and we expect small splitting of d-orbitals. As a result, after filling one electron each in lower set of orbitals, the remaining two electrons will go to the higher set of orbitals. Thus, the complex will be paramagnetic due to the presence of five unpaired electrons. It is also called high spin complex.
![Complex [Fe(CN)6]3- and [Fe(H2O)6]3+](https://classnotes.org.in/wp-content/uploads/Complex-FeCN63-and-FeH2O63-700x460.jpeg)
(2) Cobalt in [CoF6]3- and [Co(NH3)6]3+
Cobalt in [Co(NH3)6]3+and [CoF6]3-is in + 3 oxidation state and it has six d-electrons. F ion is a weak field ligand and therefore Δ° is small. The complex will be high spin. The complex is paramagnetic due to the presence of four unpaired electrons.NH3 is a strong field ligand and therefore, the electrons pair up and this results in a low spin [Co(NH3)6]3+ complex.
![Complex [CoF6]3- and [Co(NH3)6]3+](https://classnotes.org.in/wp-content/uploads/Complex-CoF63-and-CoNH363-700x372.jpeg)
Factors determining the magnitude of the orbital splitting energy Δ°
The following factors influence the magnitude of Δ°
(1) Nature of ligand: The Δ° value depends upon the nature of the ligand. The greater the ease with which the ligands can approach the metal ion and interact with it, the greater will be the crystal field splitting energy. The ligands which cause only small Δ° value are called weak field ligands while those which cause a large A value are called strong field ligands.
(2) Oxidation state of the metal ion: The higher the ionic charge on the central metal ion, the greater the value of Δ°. Therefore, the metal ion with higher oxidation state causes larger Δ° than is done by the ion with lower oxidation state.
(3) Nature of the metal ion: The A coordination entities of second and third transition series have a greater tendency to form low spin complexes as compared to the first transition series.
(4) Geometry of the coordination entity: The Δ° value for tetrahedral coordination entities is about half the Δ° value for octahedral entities i.e.
Colour in Coordination Compounds
For example: If red light (long wavelength) is absorbed from white light, then it appears to us to be green (short wavelength). If green light (short wavelength) is absorbed then it appears to us to be red.
Red and green colours are called complementary colours. Thus, the colour we see of a complex in a solid or in a solution is due to the light which is not absorbed but which is transmitted (complementary colour).
In transition metal complexes, the energy difference between two sets of d-orbitals is very small. When visible light falls on them, the electron gets raised from lower set of orbitals to higher set of orbitals.
For example: In case of octahedral complexes, the electron goes from set of dxy, dyz, dzx to set of dx2-y2 and dz2 orbitals.
As a result of absorption of some selected wavelength of visible light corresponding to energy difference between these sets of energy levels, the transmitted light gives colour to complexes.
In this complex, the metal ion has d’ configuration. In ground state this electron occupies one of the lower set of orbitals having the electronic configuration, t2g1 .The next higher energy state eg is available for the excitation of electron. When white light passes through the complex, the electron gets excited from the lower set of orbitals (t2g) to one of the higher set of orbitals, eg(dx2-y2 or dz2 orbital) by absorbing light equal to Δ°
The energy corresponding to this transition corresponds to green and yellow lights which are absorbed from the white light, while the blue and red portions are emitted. The solution of complex [Ti(H2O)6]3+, therefore, looks purple.
![Transition of one electron in [Ti(H2O)6]3+](https://classnotes.org.in/wp-content/uploads/Transition-of-one-electron-in-TiH2O63-700x263.jpeg)
The difference between different sets of orbitals in octahedral complexes vary from one metal ion to another and the nature of the ligands, therefore, different complexes absorb different amounts of energies from visible region and exhibit different colours.
According to spectrochemical series, the crystal field splitting energies will be in the order of ligands as : H2O < NH3 < CN¯
Therefore, excitation energy will be smallest (largest wavelength absorbed) for [Co(H2O)]3+ complex and largest (smallest wavelength absorbed) for [Co(CN)6]3- complex. That is why, [Co(H2O)]3+ absorbs orange colour and appears blue and [Co(CN)6]3- absorbs violet colour and appears as yellow. In the absence of ligands, the crystal field splitting does not occur and hence the substance is colourless.
For example: Removal of water from [Ti(H2O)6]Cl3 on heating makes it colourless. Similarly, anhydrous CuSO4 is white, but CuSO4⋅5H2O is blue in colour.
Example of [Ni(H2O)6]2+: This is formed when nickel chloride is dissolved in water. The aqueous solution of the complex has green colour. If the didentate ligand, ethane-1,2-diamine (en) is progressively added in the molar ratio of en : Ni as 1: 1, 2: 1 and 3: 1, the following series of reactions occur resulting different colour changes as :
[Ni(H2O)6]2+ (aq) + en (aq) → [Ni(H2O)4en]2+ + H2O
Blue / purple
These colour changes are observed due to the presence of different ligands in the complexes.
The colours of many familiar gemstones are due to the presence of transition metal ions. In these, the colours are produced due to electronic transitions within d-orbitals (called d-d transitions) of a transition metal ion.
| Transition metal | Name | Colour |
| Cr3+ ( in corundum) | Ruby | Brilliant red |
| Fe3+ ( in corundum) | Topaz (yellow sapphire) | Yellow or reddish yellow |
| Mn3+ ( in corundum) | Amethyst | Deep purple |
| Co3+ or V3+ ( in corundum) | Blue sapphire | Rui blue |
| Cr3+ (in beryl) | Emerald | Green |
| Fe3+ (in beryl) | Aquamarine | Pale blue to light greenish blue |
Leave a Reply