The feasibility of a reaction under the given experimental conditions can be predicted on, the basis of decrease in Gibbs energy (ΔG < 0). The extent to which a reaction proceeds can be explained with the help of equilibrium constant of the reaction.
The branch of chemistry which deals with the rates of chemical reactions and the factors which influence the rates of reactions is called chemical kinetics. Thermodynamics tell us only about the feasibility of a reaction whereas chemical kinetics tells us about the rate of a reaction.
The study of the rates of reactions also helps us to understand the pathways from reactants to products called mechanism of the reaction.
Contents
Rate of a chemical reaction
1) Some reactions are so rapid that they occur as soon as the reactants are mixed. The reactions involving ionic species are very fast.
For example:
a) The precipitation of silver chloride occurs very quickly on mixing the solutions of silver nitrate and sodium chloride.
b) The neutralisation of an acid by a base occurs as soon as the two substances are mixed. It may be noted that these reactions involve only the ions and no bonds are broken. Therefore, they occur very fast. These reactions occur in about 10-12 to 10-16 seconds.
2) There are certain reactions which occur at an extremely slow speed.
For example: rusting of iron occurs so slowly
3) There are some reactions which occur in a conveniently measurable time and their rates can be measured easily in the laboratory.
Examples:
(i) Hydrolysis of an ester in the presence of sodium hydroxide.
CH3COOC2H5 + NaOH—–> CH3COONa + C2H5OH
(ii) Decomposition of hydrogen peroxide
2H2O2 (aq) ———> 2H2O(l) +O2(g)
(iii) Inversion of cane sugar to give glucose and fructose
C12H22O11+H2O ———–> C6H12O6+C6H12O6
(iv) Decomposition of nitrogen (V) oxide
2N2O ——> 4 NO2 + O2
The rate of a chemical reaction is a measure of the speed with which the reactants are converted into products. It may be defined as the change in any one of the reactants or products per unit time.
R ——–>P
The rate of the reaction may be expressed in either of the following to ways:
a) The rate of disappearance or decrease in concentration of R (reactants)
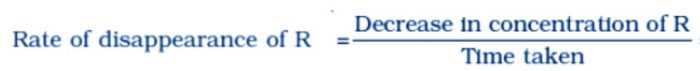
b) The rate of increase in concentration of P (products)
If [R]1 and [P]1 are the concentrations of R and P respectively at time t1, and [R]2 and [P]2 are their respective concentrations at time t2, then
Δt = t2-t1
Δ[R] = [R]2 – [R]1
and Δ[P] = [P]2 – [P]1
where the square brackets express the molar concentration and Δ[R] and Δ[P] are the changes in concentrations of R and P during time interval Δt.
Rate of reaction may be expressed as:
Rate of reaction = Δ[R] / t
Rate of reaction = Δ[P] / t
where Δ[R] gives the decrease in concentration of R and Δ[P] represents increase in concentration of P.
The square brackets around the substances are used to express the molar concentration (mol/litre).
In the case of concentration of reactants minus sign is used. This implies that the concentration of reactants is decreasing with time. The above rate is also called average rate of the reaction.
If the stoichiometric coefficients for the reactants and products are same then rate at which the concentration of R decreases will be the same as the rate at which the concentration of P increases.
1) PCl5 (g) ——> PCl3 (g)+Cl2 (g)
2) Hg(l) + Cl2 (g) ——–> HgCl2 (g)
Reactions Involving Different Stoichiometric Coefficients of Reactants & Products
Consider the reaction
A+B ——–> 2C
One mole of A reacts with one mole of B to form 2 moles of C. The rates of disappearance of A and B are same but the rate of appearance of C must be twice the rate of disappearance of A and B.
2 Rate of disappearance of A= 2 Rate of disappearance of B =Rate of appearance of C
We divide the rate of reaction defined with any of the reactants or products by the stoichiometric coefficient of that reactant or product involved in the reaction.
1) For the decomposition of gaseous nitrogen pentoxide (N2O5)
2N2O5(g) ———> 4 NO2 (g) + O2 (g)
2) 5Br¯ (aq) + BrO3¯ (aq) +6H+ (aq) ——–> 3Br2 (aq) + 3H2O(l)
For a gaseous reaction at constant temperature, concentration is directly proportional to the partial pressure of a species and hence, rate can also be expressed as rate of change in partial pressure of the reactant or the product.
Average Rate and Instantaneous Rate
The average rate of reactions over the time interval (Δt).
Rate = Change in concentration / Time interval
Rate = Δ x / Δ t
The rate depends upon the concentration of the reactants. As the reaction proceeds, the concentration of the reactants keeps on decreasing. Thus, the rate of reaction may not be constant in the time interval which we measure.
Rate of reaction may be defined as the rate of change of concentration of any one of the reactants or products at a given time. Such a reaction rate is also known as instantaneous rate.
The time interval Δt is made as small as possible So that rate of reaction remains almost constant during that time interval.
Instantaneous rates may be represented by -d[R] /dt or -d[P]/dt instead of -Δ[R]/Δt or -Δ[P]/Δt. Here d[R] or d[P] represents infinitesimally small changes in concentration of R or P in infinitesimally small interval of time dt. Thus, the average rate approaches the instantaneous rate as Δt becomes smaller and smaller i.e.
If dx represents very small (infinitesimally small) change in concentration of any species during the very small (infinitesimally small) change of time, dt, the rate of the reaction may be expressed as:
Rate of reaction = dx / dt
For a general reaction,
aA+bB = cC + dD
1) 2 N2O5 ⇔ 4 NO2 + O2
2) H2 + I2 ⇔ 2HI
3) N2 + 3 H2 ⇔ 2 NH3
Experimental Measurement of Reaction rate
The rate of a reaction can be measured by plotting a graph between the concentration of any of the reactants (or products) as a function of time.
Decomposition of dinitrogen pentoxide. It decomposes in carbon tetrachloride medium as given below :
2 N2O5 (g) ⇔ 2 N2O4 (g) + O2 (g)
This reaction can be easily studied by measuring the concentration of N2O5 at different intervals of time. The concentration at different times can be calculated by first measuring the increase in pressure of the reaction mixture at different intervals of times. From the measured values of pressure, the partial pressure of N2O5 is calculated and then the molar concentration of N2O5 can be calculated.
Then a graph is plotted between the concentration of N2O5 and time.The rate of reaction can be calculated by measuring the change in concentration during the time period.
Calculation of average rate of reaction
The average rate of reaction is determined by noting the concentration of reactants at two different times. In x1 and x2 are the concentrations in the time interval between t1 and t2.
Then average rate is:
The concentration of reactant decreases with time making (x2-x1) a negative quantity. Thus, the minus sign makes the rate as a positive quantity.
Calculation of Instantaneous rate of Reaction
The instantaneous rate gives the rate at any specific instant of time during a chemical reaction. It can be determined by drawing tangent to the curve at a point corresponding to the given time. Then the slope of this tangent gives the instantaneous rate of the reaction at that time. The slope can be determined by extending the tangent to intersect both the axes.
In the plot of concentration of reactants vs time, the tangent at any instant of time has a negative slope whereas the plot of concentration of product vs time , the tangent has a positive slope.Hence, we have,
rinst = -d[R]/dt = -slope of tangent
rinst = +d[P] /dt = slope of tangent
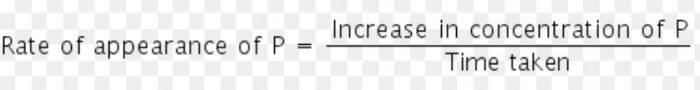
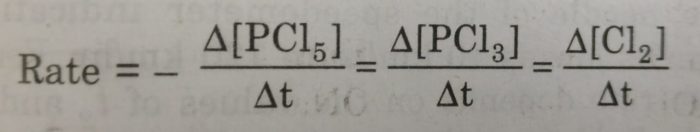
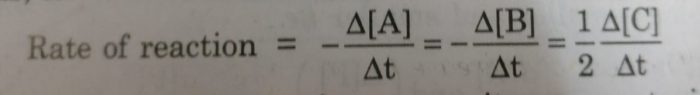
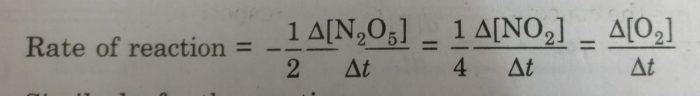
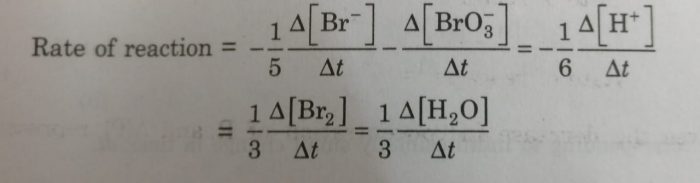
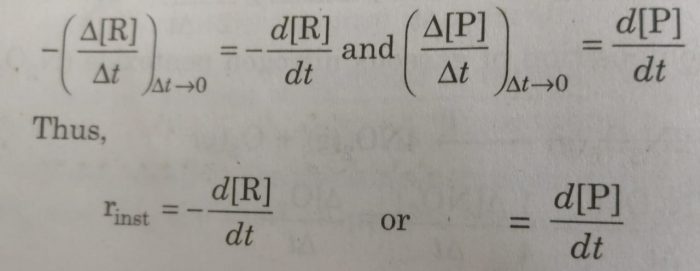
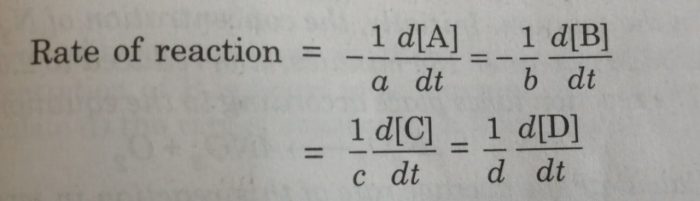
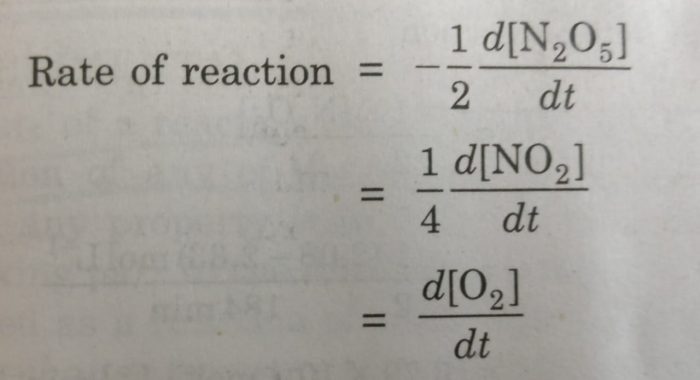
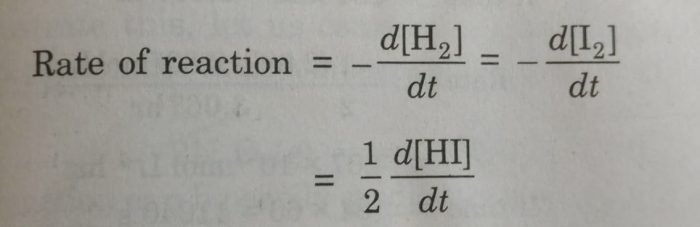
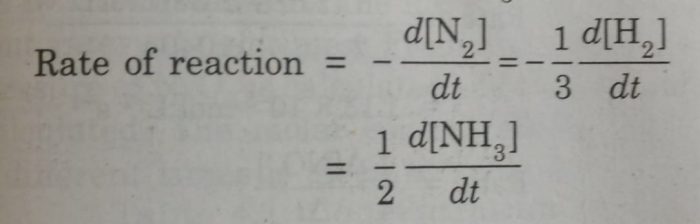
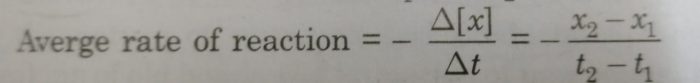
Leave a Reply