NCERT Solutions for Class 10 Maths Chapter 2 Polynomials Exercise 2.2 Page 33 1. Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients. (i) x2 – 2x – 8 (ii) 4s2 – 4s + 1 (iii) 6x2 – 3 – 7x (iv) 4u2 + 8u (v) t2 – 15 (vi) 3x2 – x – 4 (i) x2–2x –8 = x2– 4x+2x–8 = x(x–4)+2(x–4) = … [Read more...] about Exercise 2.2
Maths
Exercise 2.1
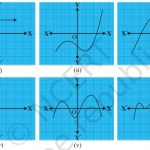
NCERT Solutions for Class 10 Maths Chapter 2 Polynomials Exercise 2.1 Page 28 1. The graphs of y = p(x) are given in Fig. 2.10 below, for some polynomials p(x). Find the number of zeroes of p(x), in each case. Answer : Graphical method to find zeroes :- Total number of zeroes in any polynomial equation = total number of times the curve intersects … [Read more...] about Exercise 2.1
Exercise 1.4
NCERT Solutions for Class 10 Maths Chapter 1 Real Numbers Exercise 1.4 Page 17 1. Without actually performing the long division, state whether the following rational numbers will have a terminating decimal expansion or a non-terminating repeating decimal expansion: (i) 13/3125 (ii) 17/8 (iii) 64/455 (iv) 15/1600 (v) 29/343 (vi) 23/(2352) (vii) 129/(225775) (viii) 6/15 … [Read more...] about Exercise 1.4
Exercise 1.3
NCERT Solutions for Class 10 Maths Chapter 1 Real Numbers Ex 1.3 Page 14 1. Prove that √5 is irrational. Answer : Let's assume, that √5 is rational number. i.e. √5 = x/y (where, x and y are co-primes) y√5= x Squaring both the sides, we get, (y√5)2 = x2 ⇒ 5y2 = x2……………………………….. (1) Thus, x2 is divisible by 5, so x is also divisible by … [Read more...] about Exercise 1.3
Exercise 1.2
NCERT Solutions for Class 10 Maths Chapter 1 Real Numbers Ex 1.2 Page 11 1. Express each number as a product of its prime factors: (i) 140 (ii) 156 (iii) 3825 (iv) 5005 (v) 7429 Answer : (i) 140 By Taking the LCM of 140, we will get the product of its prime factor. Therefore, 140 = 2 × 2 × 5 × 7 × 1 = 22×5×7 (ii) 156 By Taking the LCM of 156, we … [Read more...] about Exercise 1.2