Contents
Arrhenius Equation
Arrhenius proposed a quantitative relationship between rate constant and temperature as:
k= Ae-Ea/RT
This equation is called Arrhenius equation in which constant A is known as Arrhenius factor or frequency factor. It is also called pre-exponential factor. It is a constant specific to a particular reaction. This factor is related to number of binary molecular collisions per second per litre.
Ea is the activation energy which represents the minimum energy that the reacting molecules must possess before undergoing a reaction.
Both A and Ea are characteristic of the reaction. These are collectively called Arrhenius parameters. The factor e-Ea/RT corresponds to the fraction of molecules that have energy greater than Ea.
The value of activation energy, Ea, increases, the value of k decreases and, therefore, the reaction rate decreases.
Calculation of Activation Energy
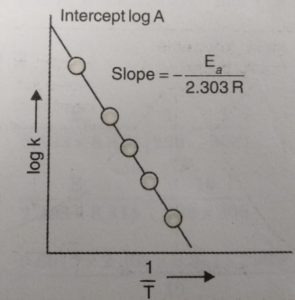
When log k is plotted against 1/T , we get a straight line. The intercept of this line is equal to log A and slope is equal to -Ea / 2.303 R.
Knowing the value of slope and gas constantR, activation energy can be calculated as :
Ea = – 2.303 R x Slope
Alternatively, Ea and A can be determined by measuring the values of rate constant at two different temperatures. Let k1 and k2 are the rate constants for the reaction at two different temperatures T1 and T2 respectively. Then,
Activation Energy and Transition State Theory
The excess energy (over and above the average energy of the reactants) which must be supplied to the reactants to undergo chemical reactions is called activation energy, Ea. It is equal to the difference between the threshold energy needed for the reaction and the average kinetic energy of all the reacting molecules. That is,
Activation energy = Threshold energy – Average kinetic energy of the reacting molecules
Ea = E (threshold) – E( reactants)
Each reaction has definite value of Ea, and this decides the fraction of total collisions which are effective.
a) If the activation energy for a reaction is low, large number of molecules can have this energy and the fraction of effective collisions, f will be large. The reaction will proceed at high rate.
b) If the activation energy is high, then fraction of effective collisions will be small and the reaction may be quite slow.
Low activation energies : Fast reactions
High activation energies : Slow reactions
Progress of a Reaction
When the colliding molecules possess the kinetic energy equal to Ea, the atomic configuration of species formed at this stage is different from the reactants as well as the products. This stage is called the activated state or transition state and specific configuration of this state is called activated complex or intermediate.
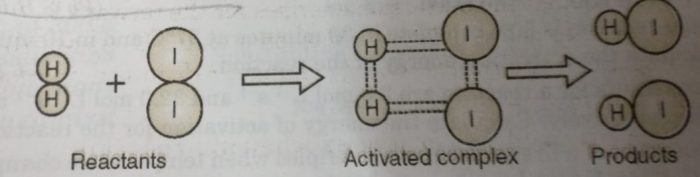
For example: In the reaction between H2(g) and I2 (g), activated complex has configuration in which H-H and I-I bonds are breaking and H-I bonds are forming.
This activated complex state is unstable transitions state of the reacting system which is mid-way between the reactants and the products. It has a very short life span (being highly unstable) and splits into the products to acquire stable state of lower energy.
Progress of a Reaction
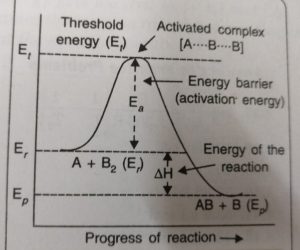
According to the concept of activation energy, the reactants first absorb energy equal to activation energy and thereby form activated complex. At this state, the molecules have energy at least equal to the threshold energy. The reaction involves some energy barrier which must be overcome before products are formed. The energy barrier is known as activation energy barrier.
The energy barrier is shown as an energy hump which has to be crossed before the reactants go to the products
A2(g) + B2(g) ——>AB(g) + B(g)
The reactants have the average energy, Er , and the products have the energy Ep. The reaction involves the approach of an atom A to a molecule B2. The reaction cannot occur until the colliding reactants A and B2, possess sufficient energy to reach the top of the energy barrier and form activated complex.
The energy required to form activated complex is called the activation energy. The activated complex formed [A….B] has a very short life span and splits into the products. This may be shown as:
A + B-B ——-> A…….B…….B ——> A-B + B
Consider the two reactions, oxidation of NO and CO. The oxidation of NO is a fast reaction whereas that of CO is a slow reaction.
NO(g) + ½ O2 (g) ——> NO2 (g) Fast
CO(g) + ½ O2 (g) ——> CO2 (g) Slow
In the oxidation of NO, the activation energy is small and only the small increase in energy enables the reacting species to cross the energy barrier to form NO2. Therefore, the reaction is fast at room temperature.
In the oxidation of CO, the activation energy is high, consequently large amount of energy is needed by the reactants to cross the energy barrier. Such a large amount of energy is not available at room temperature. Hence, the reaction is slow at room temperature.
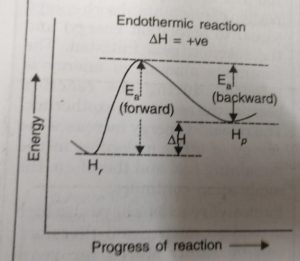
Activation Energy and Reversible Reactions
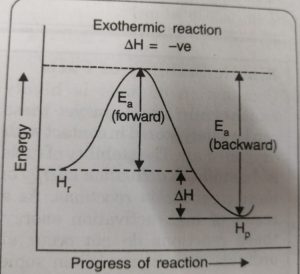
Just as activation energy is required for forward reaction, activation energy is also required for backward reaction. During the progress of the reaction the reactant molecules in the forward reaction and the product molecules in the backward reaction follow the same path and form the same activated complex.
The reactant molecules in their forward reaction and the product molecules in their backward reaction have to pass through the same transition state even though the activation energies for the forward Ea, (forward) and Eb (backward) reactions are different.
ΔH = Ea (forward) – Eb (backward)
For the exothermic reaction
Activation energy for the forward reaction < Activation energy for the backward reaction
Ea (forward) < Eb (backward)
ΔH = Ea (forward) – Eb (backward) = -ve
For the Endothermic Reaction
Activation energy for the forward reaction > Activation energy for the backward reaction
Ea (forward) > Eb (backward)
ΔH = Ea (forward) – Eb (backward) = +ve
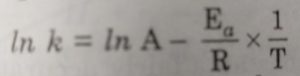
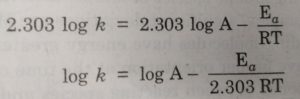
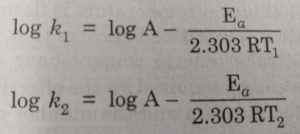
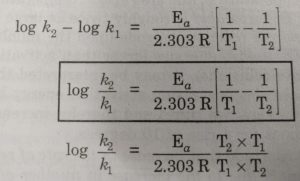
Leave a Reply