Half life period of a reaction is defined as the time during which the concentration of a reactant is reduced to half of its initial concentration.
or
The time in which half of a reaction is completed. It is generally denoted as t½
The half life period of a first order reaction may be calculated as given below:
The first order rate equation for the reaction
A ———–> Products
Now, half life period corresponds to time during which the initial concentration, [A]0 is reduced to half i.e.
[A] = [A]0 /2 at t= t½
Then half life period, t½ becomes
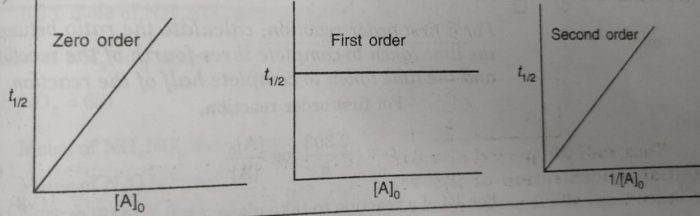
Thus, half life period of a first order reaction is independent of the initial concentration of the reactant. Half life period for the first order reaction is inversely proportional to the rate constant.
For example,
(i) time required to complete 1/3 of the reaction will be given as:
[A]o = a , [A] = a – a/3=2/3a
(ii) time required to complete 3/4 of the reaction will be
[A]o = a , [A] = a – 3/4 a = 1/4 a
Half Life period of zero order and second order reactions
The integrated rate equation is ,
kt = [A]o -[A]
For half life period, t½ , [A] = [A]0/2
t½ = [A]o /2k
Similarly for second order reaction,
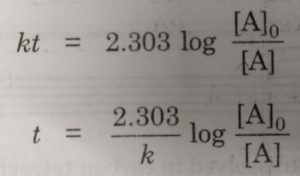
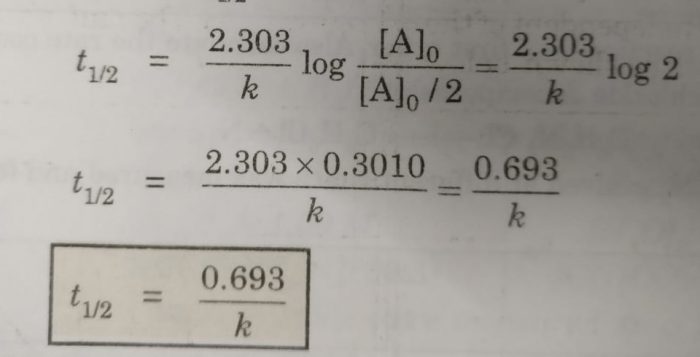

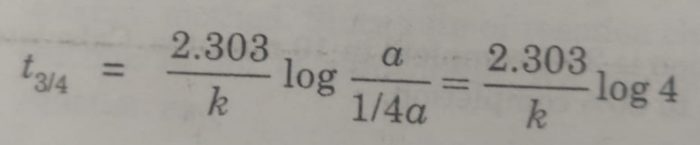
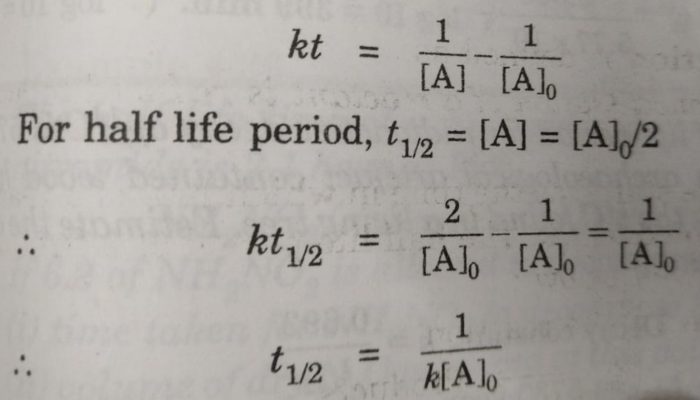
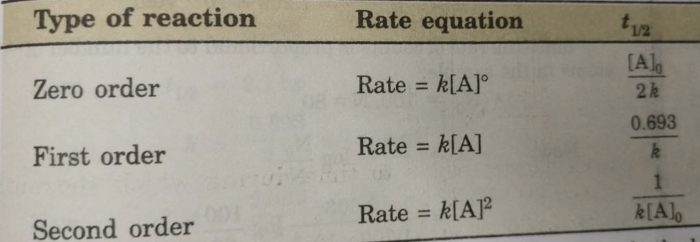
Wow very good notes is present. I understood it easily. My favourite website.
It feels very proud of this world when we looK at the faces like you
Respectful mam! Thanks alot for providing free education to all the students who are in search of this. We really appreciate your and your team’s efforts. Thanks again.
God bless you!
Keep going with this smile ☺