Contents
Integrated Rate Expression
The concentration dependence of rate is called differential rate equation. Integrated rate equation gives a relation between directly measured experimental quantities i.e. concentrations at different times. The integrated rate equations are different for reactions of different orders.
The instantaneous rate of a reaction is given by differential rate law equations.
For example: For a general reaction
aA +bB —–> Products
the differential rate law equation is :
dx/dt = k[A]a [B]b
The differential form of rate law is transformed to integrated form of rate law by simple mathematics (calculus).
Zero Order Reaction
A reaction is said to be of zero order, if its rate is independent of the concentration of the reactants. Consider the general zero order reaction:
R ——–>Product
Let [R] be the concentration of the reactant R and k0 is the rate constant for the zero order reaction. For the zero order reaction, the rate of the reaction is independent of the concentration of R. Thus
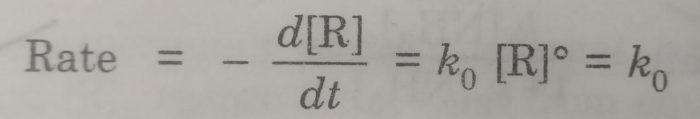
This form of rate law is known as differential rate equation, Rearranging the above equation,
-d [R] =k0 dt
Integrating the above equation
-∫ d[R] = k0 ∫ dt
-[R]= k0t + I
where I is the constant of integration. The value of I can be calculated from the initial concentration.
For example: the initial concentration of R be [R]0, at t=0
-[R]0 = k0 × 0 + I
I = – [R]0
– [R] = K0t – [R]0
K0t = [R]0 – [R]
[R] = -K0t + [R]0
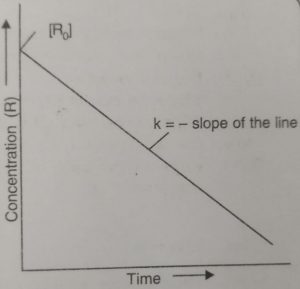
If we plot a graph between [R] against t, we get a straight line with slope as -k0 and intercept equal to [R]0.
Alternatively, rate constant, k0 can be calculated if we know the concentration of R at any time t and [R]0. Thus,
k0 = { [R]0 – [R] } / t
where [R]0, is the initial concentration of R, [R] is the concentration at time t.
Alternatively, if the initial concentration of R is ‘a’ moles per litre and let x moles of reactants get changed to products in time t. Then, concentration of R left after time t be (a – x)
R ——-> Products
[R]0 =a
[R] = a – x so that
[R]0 -[R] = a- (a-x) = x
k0 = x/t
x=k0 t
The amount of the substance reacted is proportional to the time.
Zero order reactions generally take place in heterogeneous systems. In such systems the reactant is adsorbed on the surface of a solid catalyst, where it is converted into product. The fraction of the surface of the catalyst covered by the reactant is proportional to the concentration of the reactants at low values.
After certain concentration limit of the reactant, the surface of the catalyst becomes fully covered. On further increasing the concentration of the reactant, the reaction rate does not change. The rate becomes independent of the concentration and, therefore, becomes zero order reaction.
For example: The decomposition of NH3, on the surface of finely divided platinum is first order when the pressure (or concentration) of NH3 in the system is low. However, at higher pressures (or concentrations) when the surface of the catalyst (finely divided platinum) becomes fully covered with layer of NH3, molecules, the reaction becomes zero order reaction.
2 NH3 (g) ——–> N2(g) + 3 H2 (g)
where k1 and k2 are constants. When [NH3] is very low, k2[NH3] can be neglected in comparison to unity so that the above equation becomes
Rate = k1 [NH3]
This reaction is first order in ammonia.
At higher concentration of ammonia (high pressure), we may neglect 1 as compared to [NH3] so that the equation becomes
Rate = k [NH3]
This means that rate becomes constant and independent of [NH3] and therefore, becomes zero order reaction.
Some enzyme catalysed reactions are also zero order reactions.
First order reaction
Consider the general first order reaction
R ——-> Products
Let [R] is the concentration of the reactant R and k1 is the rate constant for the first order reaction. For the first order reaction, the rate of this reaction is directly proportional to the concentration of the reactant R.
Rate = – d[R] /dt = k1 [R]
This form of rate law is known as differential rate equation. Rearranging the above equation:
– dR / [R] =k1 dt
Integrating the above equation, we get
-∫d[R] / [R] = k1 ∫dt
-ln [R] = k1t + I
where I is the constant of integration. The value of I can be calculated from the initial concentration.
For example:
The initial concentration of R be [R]0 at t=0
-ln [R]o = k × 0 × I
I = -ln [R]0
-ln [R] = k1t -ln[R]0
ln[R] = -k1t + ln [R]0
ln [R]0 -ln[R] = k1t
ln {[R]0 / [R]} = k1t
If we perform the experiment at two different times t1 and t2 having concentration [R]1 and [R]2 , then from equation, we get
ln [R]1 = -k1 t1 +ln [R]1
ln [R]2 = -k1 t2 +ln [R]0
Subtracting we get
ln [R]1 – ln [R]2 = k1 ( t2-t1)
ln {[R]1 – [R]2} = k1 ( t2-t1)
Let the initial concentration of R is ‘a’ moles per litre. Suppose in time t, x moles of reactants get changed to products. Then the concentration of R left after time t is a-x. Therefore,
[R]o = a and [R] = a – x
Significance of Integrated Rate Equation
(i) Order of reaction
All reactions of first order obey the following equation:
k1 = 2.303/t (log [R]0 / [R])
Starting with the known concentration of R, the concentration of the reactant [R], at different intervals of time (t) may be measured. The values of [R] at different time intervals are substituted in the above equation. If the value of k comes out to be constant, then the reaction is of first order.
(ii) Calculation of rate constant
If the reaction is known to be of first order, then by substituting the initial concentration of reactant [R]0 and concentrations at different times. The value of k can be calculated.
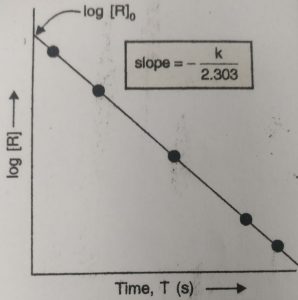
The rate constant can also be calculated graphically.
When a graph is plotted between log [R] and time t at different intervals of time we get a straight line.
Slope = -k / 2.303
From this, rate constant k, can be calculated.
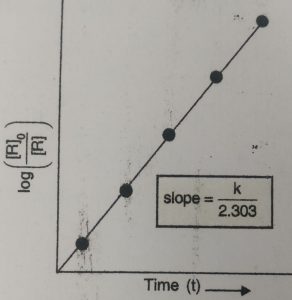
The plot of log [R]0 / [R] vs t will give a straight line with slope= k/2.303
Hydrogenation of ethene is an example of first order reaction.
C2H4 (g) +H2(g) ——> C2H6 (g)
Rate = k [C2H4]
All natural and artificial radioactive decay of unstable nuclei take place by first order kinetics.
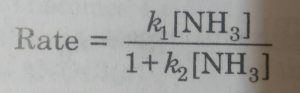
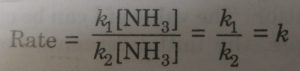
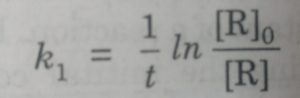
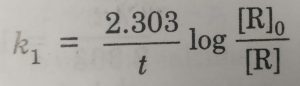
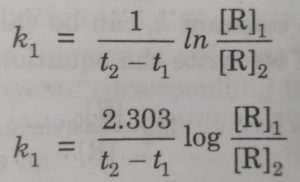
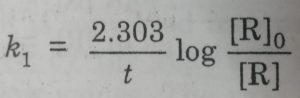
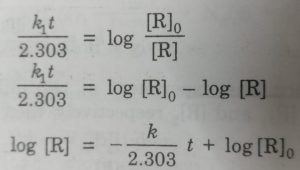
Leave a Reply