Page 200
Question 1. What does an electric circuit mean?
Answer 1 An electric circuit is the pathway in which current can flow. It consists of electric devices, switching devices, source of electricity, etc. that are connected by conducting wires.
Question 2. Define the unit of current.
Answer 2 The unit of electric current is ampere (A). When 1 C of charge flows through a conductor in 1 s, it is called 1 ampere (A) current.
I = Q /t
Question 3. Calculate the number of electrons constituting one coulomb of charge.
Answer 3 One electron possesses a charge = 1.6 × 10−19 C
Number of electron = Total charge / Charge on 1 electron
= 1/ 1.6 x 10 -19 = 6.25 × 1018
So, the number of electrons constituting one coulomb of charge is 6 × 1018
Page 202
Question 1. Name a device that helps to maintain a potential difference across a conductor.
Answer 1 A cell, battery, power supply, etc. helps to maintain a potential difference across a conductor.
Question 2. What is meant by saying that the potential difference between two points is 1 V?
Answer 2 When 1 J of work is required to move a charge of 1 C from one point to another, then it is said that the potential difference between the two points is 1 V.
V = W / Q
1Volt = 1 Joule / 1 Coulomb
Question 3. How much energy is given to each coulomb of charge passing through a 6 V battery?
Answer 3 Potential Difference = Work done / Charge
Work done (or Energy) = Potential difference × Charge
So, Work done = 6 Volt × 1 Coulomb = 6 Joule.
Page 209
Question 1. On what factors does the resistance of a conductor depend?
Answer 1 The resistance of a conductor depends upon the following factors:
(i) Length of the conductor.
(ii) Cross-sectional area of the conductor.
(iii) Material of the conductor.
(iv) Temperature of the conductor.
Question 2. Will current flow more easily through a thick wire or a thin wire of the same material, when connected to the same source? Why?
Answer 2 Resistance (R) is inversely proportional to the area of cross-section (A) of the wire.
So, thicker the wire, lower is the resistance of the wire and vice-versa.
Therefore, current can flow more easily through a thick wire than a thin wire.
R = ρ x (L/A)
R ∝ 1/A
ρ = Resistivity of material of wire
L = length of the wire
Question 3. Let the resistance of an electrical component remains constant while the potential difference across the two ends of the component decreases to half of its former value. What change will occur in the current through it?
Answer 3 According to the Ohm’s law V = IR
If the resistance remains constant, V is directly proportional to I.
Therefore, V ∝ I
Now, if potential difference is reduced to half of its value, the current also become half of its original value.
Question 4. Why are coils of electric toasters and electric irons made of an alloy rather than a pure metal?
Answer 4 The resistivity of an alloy is higher than the pure metal and it does not corrode easily. Moreover, even at high temperatures, the alloys do not melt readily.
Hence, the coils of heating appliances such as electric toasters and electric irons are made of an alloy rather than a pure metal.
Question 5. Use the data in Table 12.2 to answer the following –
(a) Which among iron and mercury is a better conductor?
(b) Which material is the best conductor?
| Conductors |
Material | Resistivity ( Ωm) |
| Silver | 1.60 x 10-8 | |
| Copper | 1.02 x 10-8 | |
| Aluminium | 2.63 x 10-8 | |
| Tungsten | 5.20 x 10-8 | |
| Nickel | 6.84 x 10-8 | |
| Iron | 10.0 x 10-8 | |
| Chromium | 12.9 x 10-8 | |
| Mercury | 94.0 x 10-8 | |
| Manganese | 1.84 x 10-8 | |
| Alloys | Constantan (alloy of Cu and Ni) | 49 x 10-6 |
| mangane in (allay at Cu, Mn, and Ni) | 44 x 10-6 | |
| Nichrome (alloy of Ni, Cr, Mn, and Fe) | 100 x 10-6 | |
| Insulators | Glass | 1010 – 1014 |
| Hard Rubber | 1013 – 1016 | |
| Ebonite | 1015 – 1017 | |
| Diamond | 1012 – 1013 | |
| Paper (dry) | 1012 |
Answer 5 (a) Resistivity of iron (10 × 10-8 Ωm ) is lesser than that of the mercury (94 × 10-8 Ωm).So, iron is a good conductor as compared to mercury.
(b) Silver has lowest resistivity , so it is the best conductor.
Page 213
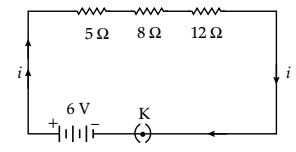
Question 1. Draw a schematic diagram of a circuit consisting of a battery of three cells of 2 V each, a 5 W resistor, an 8 W resistor, and a 12 W resistor, and a plug key, all connected in series.
Answer 1 The required schematic diagram is given below:
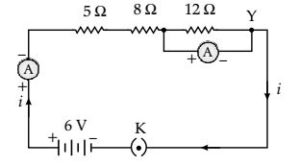
Question 2. Redraw the circuit of Question 1, putting in an ammeter to measure the current through the resistors and a voltmeter to measure the potential difference across the 12 W resistor. What would be the readings in the ammeter and the voltmeter?
Answer 2 Resisters are connected in series.
So, the net resistance in the circuit = 5 Ω + 8 Ω + 12 Ω = 25 Ω
Net potential = 6 V
Using Ohm’s law V = IR, we have
6 =I × 25
I=6/25= 0.24 Ampere
Now for the 12 Ω resistor, current = 0.24 Ampere
So, using Ohm’s law
V = 0.24 × 12 V = 2.88 V
Hence, the reading in the ammeter is 0.24 amp and voltmeter is 2.88 volt.
Page 216
Question 1. Judge the equivalent resistance when the following are connected in parallel – (a) 1 W and 106 W
(b) 1 W and 103 W, and 106 W.
Answer 1 (a) The net resistance in parallel is given by
1/R = 1/ R1 + 1 / R2
Here, R1 = 1 Ω and R2 = 106 Ω
1/R = 1/1 + 1/106 = (106 + 1) / 106
⇒ R = 106 / 106 + 1 = 1 Ω
(b) The net resistance in parallel is given by
1/R = 1/R1 + 1/R2 +1/R3
R1 = 1 Ω , R2= 103 Ω , R3 = 106 Ω
1/R = 1/1 + 1/103 +1/106
1/R =( 1+103 +106) /106
1/R = 1001001/1000000
1/R =0.9999 Ω =1 Ω
Question 2. An electric lamp of 100 W, a toaster of resistance 50 W, and a water filter of resistance 500 W are connected in parallel to a 220 V source. What is the resistance of an electric iron connected to the same source that takes as much current as all three appliances, and what is the current through it?
Answer 2 Given that the electric lamp of 100 Ω, a toaster of resistance 50 Ω and water filter of resistance 500 Ω are connected in parallel.
The net resistance in parallel is given by
1/R = 1/R1 + 1/R2 + 1/R3
Here, R1 = 100 Ω, R2 = 50, R3 = 500 Ω
1/R = 1/100 + 1/50 + 1/500 = (5 + 10 + 1 )/ 500 = 16 /500
⇒ R = 500/ 16 = 31·25 Ω
According to Ohm’s Law V=IR
I=V/R
I=220/31.25
I=7.04 A
Question 3. What are the advantages of connecting electrical devices in parallel with the battery instead of connecting them in series?
Answer 3 In parallel there is no division of voltage among the appliances. The potential difference across each appliance is equal to the supplied voltage and the total effective resistance of the circuit can be reduced by connecting electrical appliances in parallel.
Question 4. How can three resistors of resistances 2 W, 3 W, and 6 W be connected to give a total resistance of (a) 4 W, (b) 1 W?
Answer 4 (a) To get total resistance 4 Ω, connect 3 Ω and 6 Ω resistors in parallel and 2 Ω resistance in series with the resultant.
Since, 3 Ω and 6 Ω resistors are in parallel, so the net resistance will be
1/R12 = 1/R1 +1/R2
1/R12 = 1/3 + 1/6 = (2+1)/6 = 3/6 = 1/2 Ω
⇒ R12 = 2 / 1 = 2 Ω
Now, the resultant R12 and 2 Ω resistors are in series.
So, the net resistance R = R12+2 Ω = 2 + 2 = 4 Ω
(b) To get total resistance 1 Ω, connect 2 Ω, 3 Ω and 6 Ω resistors in parallel.
The net resistance in parallel is given by
1/R = 1/R1 + 1/R2 + 1/R3
Here, R1=2 Ω, R2 = 3 Ω and R3 = 6 Ω So,
1/R = 1/2 +1/3 + 1/6
= (3+2+1)/ 6 = 6/6 Ω
⇒ R = 6/6 = 1 Ω
Question 5. What is (a) the highest, (b) the lowest total resistance that can be secured by combinations of four coils of resistance 4 W, 8 W, 12 W, 24 W?
Answer 5 Connecting resistors in series always gives maximum resistance and parallel gives minimum resistance.
(a) The highest total resistance is given by
R = R1 + R2 + R3 + R4
= 4 Ω + 8 Ω + 12 Ω + 24 Ω = 48 Ω
(b) The lowest total resistance is given by
1/R = 1/R1 + 1/R2 + 1/R3 + 1/R4
1/R = 1/4 + 1/8 + 1/12 + 1/24 = (6+3+2+1)/24 = 12/24
R = 24/12 = 2 Ω
Page 218
Question 1. Why does the cord of an electric heater not glow while the heating element does?
Answer 1 The heating element of an electric heater is a resistor. According to Joule’s law of heating, the amount of heat produced by it is proportional to its resistance.
H = I2 Rt
The resistance of the element of an electric heater is very high. As current flows through the heating element, it becomes too hot and glows red. On the other hand, the resistance of the cord is low. It does not become red when current flows through it.
Question 2. Compute the heat generated while transferring 96000 coulomb of charge in one hour through a potential difference of 50 V.
Answer 2 According to Joule’s law of heating, the amount of heat produced is given by
H = V × I × t
Where, V = 50 V
I = Charge/Time = 9600 Coulomb/1 hr
= 9600/ (60 x 60) = 80/3 A
and t = 1 hour = 60 × 60 sec
So, H = 50 x (80/ 3) × × 60 × 60 = 4800000 J
= 4.8 × 106 J
Question 3. An electric iron of resistance 20 W takes a current of 5 A. Calculate the heat developed in 30 s.
Answer 3 According to Joule’s law of heating, the amount of heat produced is given by
H = V I t
Where, V= I R = 5 A × 20 Ω = 100 V
I = 5A
t = 30 Seconds
So, H = 100 × 5 × 30 J
= 15000 J = 1.5 × 104 J
Page 220
Question 1. What determines the rate at which energy is delivered by a current?
Answer 1 The rate of consumption of electric energy in an electric appliance is called electric power. Hence, the rate at which energy is delivered by a current is the power of the appliance.
Question 2. An electric motor takes 5 A from a 220 V line. Determine the power of the motor and the energy consumed in 2 h.
Answer 2 Power of the electric motor is given by:
P = VI Where, V = 220 V and I = 5 A
So, Power P = 220 × 5 = 1100 W
Now, the energy consumed = Power × time Where, P = 1100 W
t = 2 hours = 2 × 60 × 60 seconds = 7200 seconds
So, the energy consumed E = 1100 × 7200 J = 79,20,000 J
Page 221-222
Question 1. A piece of wire of resistance R is cut into five equal parts. These parts are then connected in parallel. If the equivalent resistance of this combination is R’, then the ratio R/R’ is –
(a) 1/25 (b) 1/5 (c) 5 (d) 25
Answer 1 (d) 25
All the five parts are connected in parallel. Hence, equivalent resistance (R′) is given as
1/R’ = 1/(R/5) + 1/(R/5) + 1/(R/5) + 1/)R/5) + 1/(R/5)
⇒ 1/R’= 5/R + 5/R + 5/R + 5/R + 5/R = 25/R
⇒ R’ = R/25
⇒ R’/R = 1/25
So, R/R’ = 25
Question 2. Which of the following terms does not represent electrical power in a circuit?
(a) I2R (b) IR2 (c) VI (d) V2/R
Answer 2 (b) IR2
P = VI… (i)
So, the option (c) is correct.
According to Ohm’s law, V = IR… (ii)
Now putting the value of V from (ii) in (i), we get
Power P = (IR) × I = I2 R So, the option (a) is correct.
Now putting the value of I from (ii) in (i), we get Power P = V(V/R) = V2 /R
so, option (d) is correct.
Hence , the option (b) does not represent electrical power in a circuit.
Question 3. An electric bulb is rated 220 V and 100 W. When it is operated on 110 V, the power consumed will be –
(a) 100 W (b) 75 W (c) 50 W (d) 25 W
Answer 3 (d) 25 W
As we know that the energy consumed by bulb
⇒ P = V2/R
⇒R = V2/P
where, V = 220 volt and P = 100 watt
R = (220)2 /100 = 484 Ω
The resistance of the bulb remains constant if the supply voltage is reduced to 110 V.
If the bulb is operated on 110 V, then the energy consumed by it is given by the expression for power
P = V2/R = (110)2/484= 12100/484= 25 W
Question 4. Two conducting wires of the same material and of equal lengths and equal diameters are first connected in series and then parallel in a circuit across the same potential difference. The ratio of heat produced in series and parallel combinations would be –
(a) 1:2 (b) 2:1 (c) 1:4 (d) 4:1
Answer 4 (c) 1:4
Heat produced in the circuit is inversely proportional to the resistance R. Let RS and RP be the equivalent resistances of the wires if connected in series and parallel, respectively. Let R be the resistance of each wire. If the resistors are connected in parallel, the net resistance is given by
1/Rp= 1/R+ 1/R
⇒1/Rp = 2/R
⇒Rp = R/2
If the resistors are connected in series, the net resistance is given by
Rs = R + R = 2R
Hence for same potential difference V, the ratio of heat produced in the circuit is given by
Hs/Hp =[( V2/Rs) x t ] / [(V2/Rp) x t] = Rp/ RS = R/2/2R = 1/4 = 1:4
Therefore, the ratio of heat produced in series and parallel combinations is 1: 4
Question 5. How is a voltmeter connected in the circuit to measure the potential difference between two points?
Answer 5 A voltmeter must always be connected in parallel to measure the potential difference between two points.
Question 6. A copper wire has diameter 0.5 mm and resistivity of 1.6 × 10–8 W m. What will be the length of this wire to make its resistance 10 W? How much does the resistance change if the diameter is doubled?
Answer 6 Resistance (R) of a copper wire length l and cross-section A is given by the expression.
R = ρ x (l/A)
where, ρ is resistivity of copper = 1.6 × 10–8 Ω m. R= 10 Ω,
Radius of wire r = 0.5/2 mm = 0.25 mm = 0.00025 m.
A=πr2= 3.14 x (0.00025)2 = 0.000000019625 m2
⇒ l = RA/ρ= (10 x 0.000000019625 )/ 1.6 x 10-8
=122.72 m
If the diameter (radius) is doubled, the new radius
r = 0.5mm = 0.0005m
A=πr2
=3.14 x (0.0005)2
= 0.000000785 m2
So, the new resistance will be
⇒ R’ = ρl/A= (1.6 x 10-8 x 122.72) / 0.000000785
= 2.5 Ω
R’/R = 0.25/ 10 = 1/4
⇒R’ = 1/4 R
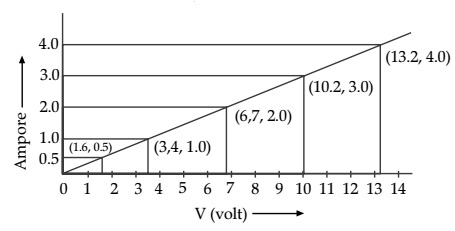
Question 7. The values of current I flowing in a given resistor for the corresponding values of potential difference V across the resistor are given below –
| I (amperes) | 0.5 | 1.0 | 2.0 | 3.0 | 4.0 |
| V (volts) | 1.6 | 3.4 | 6.7 | 10.2 | 13.2 |
Plot a graph between V and I and calculate the resistance of that resistor.
Answer 7 The plot between voltage and current is called VI characteristics. The voltage is plotted on x-axis and current is plotted on y-axis.
The slope of the line gives the value of resistance (R) So the resistance of the resistor
R = (V2-V1)/ (I2-I1)= (6.7- 3.4)/(2.0- 1.0)
R = 3.3V/ 1.0 A
R= 3.3 ohm
Question 8. When a 12 V battery is connected across an unknown resistor, there is a current of 2.5 mA in the circuit. Find the value of the resistance of the resistor.
Answer 8 According to Ohm’s law,
V = IR
⇒ R = V/I
Here, V = 12V and I = 2.5 mA = 0.0025 A
Therefore, R=V/I
R= 12/ 0.0025
R= 4800 Ω
R= 4.8 KΩ
Question 9. A battery of 9 V is connected in series with resistors of 0.2 W, 0.3 W, 0.4 W , 0.5 W and 12 W, respectively. How much current would flow through the 12 W resistor?
Answer 9 Total resistance of resistors when connected in series is given by R = R1 + R2 + R3 + R4 + R5
R= 0.2 Ω + 0.3 Ω + 0.4 Ω + 0.5 Ω + 12 Ω
According to Ohm’s Law, V=IR
⇒ I= V/R = 9/13.4= 0.67 Amp
There is no current division occurring in a series circuit.
So, the current through the 12 ohm resistor will be same as 0.67 amp.
Question 10. How many 176 W resistors (in parallel) are required to carry 5 A on a 220 V line?
Answer 10 Let the total number of resistors be x.
Given that, Current I = 5A and the potential difference V = 220 V
According to Ohm’s law, V = IR
⇒ R = V/I = 220/5 = 44 Ω
Now for x number of resistors of resistance 176 Ω, the equivalent resistance of the resistors connected in parallel is 44 Ω
1/44 = 1/176+ 1/176+1/176+1/176+……..to x times
⇒1/44 = x/176
⇒x = 176/44= 4
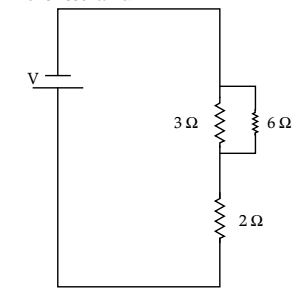
Question 11. Show how you would connect three resistors, each of resistance 6 W, so that the combination has a resistance of (i) 9 W, (ii) 4 W.
Answer 11 (i) To get total 9 Ω resistance from three 6 Ω resistors, we should connect two resistors in parallel and the third resistor in series with the resultant. The combination is given as follows:
Total resistance is given by
1/R12= 1/R1+1/R2
⇒1/R12= 1/6+1/6= 2/6=1/3
⇒ R12 = 3 Ω
Now R12 and 6 Ω are connected in series, so the net resistance is given by
R = R12 + 6 Ω = 3 Ω +6 Ω = 9 Ω
(ii) To get total 4 Ω resistance from three 6 Ω resistors, we should connect two resistors in series and the third resistor in parallel with the resultant. The combination is given as follows:
Total resistance in series is given by
R12 = R1 + R2 = 6 Ω + 6 Ω = 12 Ω
Now R12 and 6 Ω are connected in parallel,
so the net resistance is given by
⇒ 1/R= 1/R12+ 1/6
⇒ 1/R = 1/R12+ 1/6= 3/12= 1/4
= R = 4 Ω
Question 12. Several electric bulbs designed to be used on a 220 V electric supply line, are rated 10 W. How many lamps can be connected in parallel with each other across the two wires of 220 V line if the maximum allowable current is 5 A?
Answer 12 For one bulb: Power P = 10 W and Potential difference V = 220 V
Using the relation for R, we have
R= V/P = (220)2/10 = 4840 Ω
Let the total number of bulbs be x. Given that:
Current I = 5 A and Potential Difference V = 220 V
According to Ohm’s Law V = IR
⇒ V/P= 220/5 = 44 Ω
Now, for x number of bulbs of resistances 176 Ω the equivalent resistance of the resistors connected in parallel is 44 Ω
1/44= 1/4840 +1/4840 +1/4840 +…….. to x times
⇒ 1/44= x/4840
x= 4840/44= 110
Therefore, 110 bulbs of 4840 Ω are required to draw the given amount of current.
Question 13. A hot plate of an electric oven connected to a 220 V line has two resistance coils A and B, each of 24 W resistance, which may be used separately, in series, or in parallel. What are the currents in the three cases?
Answer 13 Potential difference V = 220 V and resistance of each coil R = 24 Ω
When the coil is used separately, the current in the coil is given by
I= V /R = 220/24 = 55/6 = 9.16 A
When the two coils are connected in series, the net resistance is given by
R = R1 + R2 = 24 Ω + 24 Ω = 48 Ω
Now, the current in the coil is given by
I = V/R = 220/48 = 55/12 = 4.58 A
When the two coils are connected in parallel, the net resistance is given by
1/R= 1/24 +1/24 =2/24=1/12
⇒ R = 12 Ω
Now, the current in the coil is given by
⇒ I = V/R = 220/12 = 55/3 = 18.33 A
Question 14. Compare the power used in the 2 W resistor in each of the following circuits:
(i) a 6 V battery in series with 1 W and 2 W resistors, and (ii) a 4 V battery in parallel
with 12 W and 2 W resistors.
Answer 14 Potential difference, V = 6 V
(i) 1 Ω and 2 Ω resistors are connected in series.
Therefore, equivalent resistance of the circuit, R = 1 + 2 = 3 Ω
According to Ohm’s law, V = IR
⇒ I = V / R = 6 / 3 = 2A
In series combination, the current in the circuit remains constant.
Therefore, power is given by P = I2 R = (2)2 × 2 = 8 W
(ii) 1 Ω and 2 Ω resistors are connected in parallel. ⇒ I = V/R = 6 /3 = 2 A
In parallel combination, the voltage in the circuit remains constant.
Therefore, power is given by P = V2 R = 42/ 2 = 8 W
Here, in both cases power will be same as 8 W.
Question 15. Two lamps, one rated 100 W at 220 V, and the other 60 W at 220 V, are connected in parallel to electric mains supply. What current is drawn from the line if the supply voltage is 220 V?
Answer 15 For the Lamp one: Power P1 = 100W and Potential Difference V = 220 V
Therefore, I1 = P1 /V =100 / = 0.455 A
For the Lamp two: Power P2 = 60 W and potential Difference V = 220 V
Therefore, I2 = P2/ V = 60 / 220 = 0.273
So, the net current drawn from the power supply is given by I = I1 + I2 = 0.455 + 0.273 = 0.728 A
Question 16. Which uses more energy, a 250 W TV set in 1 hr, or a 1200 W toaster in 10 minutes?
Answer 16 For T.V set Power (P) = 250 W,
Time (t) = 1 hr=60×60=3600 s
For Toaster Power (P) = 1200 W, Time (t) = 10 min=10×60=600 s
We know that Energy (E) = P×t
∴ Energy consumed by a TV set = 250 × 3600 = 9 × 105 J
∴ Energy consumed by a toaster = 1200 × 600 = 7.2× 105 J
∴ The energy consumed by a 250 W TV set in 1 h is more than the energy consumed by a toaster of power 1200 W in 10 minutes.
Question 17. An electric heater of resistance 8 W draws 15 A from the service mains 2 hours.Calculate the rate at which heat is developed in the heater.
Answer 17 Heat developed in the heater is given by
H = I2 Rt Where, I = 15 A, R = 8 Ω and time t = 2 hours
The rate at which heat is developed is given by:
H = I2 Rt/t =I2 R = (15)2 × 8 = 1800 J/s
Question 18. Explain the following.
(a) Why is the tungsten used almost exclusively for filament of electric lamps?
(b) Why are the conductors of electric heating devices, such as bread-toasters and electric irons, made of an alloy rather than a pure metal?
(c) Why is the series arrangement not used for domestic circuits?
(d) How does the resistance of a wire vary with its area of cross-section?
(e) Why are copper and aluminium wires usually employed for electricity transmission?
Answer 18
(a) The melting point and resistivity of tungsten are very high. It does not burn readily at a high temperature. The electric lamps glow at very high temperatures. Hence, tungsten is mainly used as heating element of electric bulbs.
(b) The conductors of electric heating devices such as bread toasters and electric irons are made of alloy because resistivity of an alloy is more than that of metals. It produces large amount of heat and do not burn easily.
(c) There is voltage division in series circuits. Each component of a series circuit receives a small voltage for a large supply voltage. As a result, the amount of current decreases and the device becomes hot. Hence, series arrangement is not used in domestic circuits.
(d) Resistance (R) of a wire is inversely proportional to its area of cross-section (A):
R ∝ 1/A
(e) Copper and aluminium wires have low resistivity. They are good conductors of electricity. Hence, they are usually employed for electricity transmission.
Leave a Reply