Exercise 3.7

NCERT Solutions for Class 10 Maths Chapter 3
Pair of Linear Equations in Two Variables
Exercise 3.7 (Optional)

Page 68

1. The ages of two friends Ani and Biju differ by 3 years. Ani’s father Dharam is twice as old as Ani and Biju is twice as old as his sister Cathy. The ages of Cathy and Dharam differ by 30 years. Find the ages of Ani and Biju.

The age difference between Ani and Biju is 3 years

Either Biju is 3 years older than that of Ani or Ani is 3 years older than Biju.

From both the cases we find out that Ani’s father’s age is 30 years more than that of Cathy’s age.

Let the ages of Ani and Biju be A and B respectively.

Therefore, the age of Dharam = 2 x A = 2A years.

And the age of Biju sister Ann B/2 years

By using the information that is given,

Case (i)

When Ani is older than that of Biju by 3 years then A – B = 3 …..(i)

2A−B/2 = 30

4A – B = 60 …..(ii)

By subtracting the equations (i) and (ii) we get,

3A = 60 – 3 = 57

A = 57/3 = 19

 

Therefore, the age of Ani = 19 years

And the age of Biju is 19 – 3 = 16 years.

Case (ii)

When Biju is older than Ani,

B – A = 3 …..(iii)

2A − B/2 = 30

4A – B = 60 …..(iv)

Adding the equation (iii) and (iv) we get,

3A = 63

A = 21

Therefore, the age of Ani is 21 years

And the age of Biju is 21 + 3 = 24 years.

2. One says, “Give me a hundred, friend! I shall then become twice as rich as you”. The other replies, “If you give me ten, I shall be six times as rich as you”. Tell me what is the amount of their (respective) capital? [From the Bijaganita of Bhaskara II] [Hint : x + 100 = 2(y – 100), y + 10 = 6(x – 10)].

Let Sangam have ₹ A with him and Reuben have ₹ B with him.

Using the information that is given we get,

A + 100 = 2(B – 100) ⇒ A + 100 = 2B – 200

Or A – 2B = -300  …..(i)

And

6(A – 10) = ( B + 10 )

Or 6A – 60 = B + 10

Or 6A – B = 70 …..(i)

When equation (2) is multiplied by 2 we get,

12A – 2B = 140  …..(iii)

When equation (i) is subtracted from equation (iii) we get,

11A = 140 + 300

11A = 440

⇒ A = 440/11 = 40

Using A =40 in equation (i) we get,

40 – 2B = -300

40 + 300 = 2B

2B = 340

B = 170

Therefore, Sangam had ₹ 40 and Reuben had ₹ 170 with them.

 

3. A train covered a certain distance at a uniform speed. If the train would have been 10 km/h faster, it would have taken 2 hours less than the scheduled time. And, if the train were slower by 10 km/h; it would have taken 3 hours more than the scheduled time. Find the distance covered by the train.

Let the speed of the train be A km/hr and the time taken by the train to travel a distance be N hours and the distance to travel be X hours.

Speed of the train = Distance travelled by train / Time taken to travel that distance

A = N (distance)/ X (time)

Or, N = AX …..(i)

Using the information that is given, we get:

(A+10) = X/(N-2)

(A + 10) (N – 2) = X

AN + 10N – 2A – 20 = X

By using the equation (1) we get,

– 2A + 10N = 20  …..(ii)

(A-10) = X/(N+3)

(A – 10) (N + 3) = X

AN – 10N + 3A – 30 = X

By using the equation (1) we get,

3A – 10N = 30  …..(iii)

Adding equation (ii) and equation (iii) we get,

A = 50

Using the equation (ii) we get,

(-2) x (50) + 10N = 20

-100 +10N = 20

⇒ 10N = 120

N = 12hours

From the equation (i) we get,

Distance travelled by the train, X = AN

= 50 x 12

= 600 km

Hence, the distance covered by the train is 600km.

 

4. The students of a class are made to stand in rows. If 3 students are extra in a row, there would be 1 row less. If 3 students are less in a row, there would be 2 rows more. Find the number of students in the class.

Let the number of rows be A and the number of students in a row be B.

Total number of students = Number of rows x Number of students in a row

= AB

Using the information, that is given,

First Condition:

Total number of students = (A – 1) ( B + 3)

Or AB = ( A – 1 )(B + 3) = AB – B + 3A – 3

Or 3A – B – 3 = 0

Or 3A – Y = 3 …..(i)

Second condition:

Total Number of students = (A + 2 ) ( B – 3 )

Or AB = AB + 2B – 3A – 6

Or 3A – 2B = -6 …..(ii)

When equation (ii) is subtracted from (i)

(3A – B) – (3A – 2B) = 3 – (-6)

-B + 2B = 3 + 6B = 9

By using the equation (i) we get,

3A – 9 =3

3A = 9+3 = 12

A = 4

Number of rows, A = 4

Number of students in a row, B = 9

Number of total students in a class = AB = 4 x 9 = 36

5. In a ∆ABC, ∠ C = 3 ∠ B = 2 (∠A + ∠ B). Find the three angles.

Given,

∠C = 3 ∠B = 2(∠B + ∠A)

∠B = 2 ∠A+2 ∠B

∠B=2 ∠A

∠A – ∠B= 0 …..(i)

We know, the sum of all the interior angles of a triangle is 180^O.

Thus, ∠ A +∠B+ ∠C = 180^O

∠A + ∠B +3 ∠B = 180^O

∠A + 4 ∠B = 180^O …..(ii)

Multiplying 4 to  equation (i) , we get

8 ∠A – 4 ∠B = 0  …..(iii)

Adding equations (iii) and (ii) we get

9 ∠A = 180^O

∠A = 20^O

Using this in equation (ii), we get

20^O+ 4∠B = 180^O

∠B = 40^O

3∠B =∠C

∠C = 3 x 40 = 120^O

Therefore, ∠A = 20^O

∠B=40^O

∠C = 120^O

 

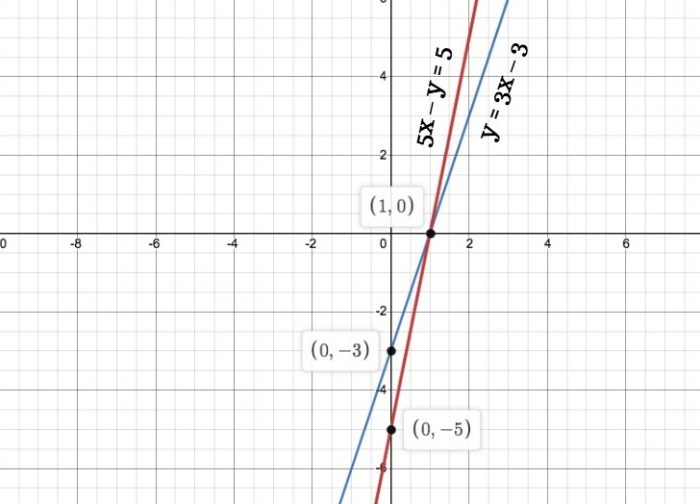
6. Draw the graphs of the equations 5x – y = 5 and 3x – y = 3. Determine the co-ordinates of the vertices of the triangle formed by these lines and the y axis.

Given,

5x – y = 5

⇒ y = 5x – 5

Its solution table will be.

x	2	1	0
y	5	0	-5

Also given, 3x – y = 3

y = 3x – 3

x	2	1	0
y	5	0	-5

The graphical representation of these lines will be as follows:

From the above graph we can see that the triangle formed is ∆ABC by the lines and the y axis.

Also the coordinates of the vertices are A(1,0) ,  C(0,-5) and B(0,-3).

7. Solve the following pair of linear equations:

(i) px + qy = p – q

qx – py = p + q

px + qy = p – q …..(i)

qx – py = p + q …..(ii)

Multiplying p to equation (i)  and q to equation (ii), we get

p²x + pqy = p² − pq …..(iii)

q²x − pqy = pq + q² …..(iv)

Adding equation (iii) and equation (iv),we get

p²x + q² x = p²  + q²

(p² + q² ) x = p² + q²

x = (p² + q²)/ p² + q² = 1

From equation (i), we get

p(1) + qy = p – q

qy = p-q-p

qy = -q

y = -1

 

(ii) ax + by = c

bx + ay = 1 + c

ax + by= c …..(i)

bx + ay = 1+ c. …..(ii)

Multiplying a to equation (i) and  b to equation (ii), we obtain

a²x + aby = ac …..(iii)

b²x + aby = b + bc …..(iv)

Subtracting equation (iv) from equation (iii),

(a² – b²) x = ac − bc– b

x = (ac − bc– b)/ (a² – b²)

x = c(a-b) –b / (a²+b²)

From equation (i), we obtain

ax +by = c

a{c(a−b)−b)/ (a² – b²)} +by=c

ac(a−b)−ab/ (a² – b²)+by=c

by=c–ac(a−b)−ab/(a² – b²)

by=abc – b² c+ab/a²-b²

y = c(a-b) + a/(a²-b²)

(iii) x/a – y/b = 0

ax + by = a² + b²

x/a – y/b = 0

=> bx − ay = 0  …..(i)

ax + by = a² + b² …..(ii)

Multiplying a and b to equation (i) and (ii) respectively, we get

b²x − aby = 0 …..(iii)

a²x + aby = a ³ + ab³ …..(iv)

Adding equations (iii) and (iv), we get

b²x + a²x = a ³ + ab²

x (b² + a²) = a (a² + b²) x = a

Using equation (i), we get

b(a) − ay = 0

ab − ay = 0

ay = ab,

y = b

 

(iv) (a – b)x + (a + b) y = a² – 2ab – b²

(a + b)(x + y) = a² + b²

(a + b) y + (a – b) x = a²− 2ab − b² …..(i)

(x + y)(a + b)  = a ² + b²

(a + b) y + (a + b) x  = a² + b² …..(ii)

Subtracting equation (ii) from equation (i), we get

(a − b) x − (a + b) x = (a ² − 2ab − b ²) − (a² + b²)

x(a − b − a − b) = − 2ab − 2b²

− 2bx = − 2b (b + a)

x = b + a

Substituting this value in equation (i), we get

(a + b)(a − b)  +y (a + b)  = a²− 2ab – b²

a² − b² + y(a + b)  = a²− 2ab – b²

(a + b) y = − 2ab

y = -2ab/(a+b)

(v) 152x − 378y = − 74

76x − 189y = − 37

x =(189y-137)/76 …..(i)

− 378x + 152y = − 604

− 189x + 76y = − 302  …..(ii)

Using the value of x in equation (ii), we get

−189(189y−37/76)+76y=−302

− (189)²y + 189 × 37 + (76)² y = − 302 × 76

189 × 37 + 302 × 76 = (189)² y − (76)²y

6993 + 22952 = (189 − 76) (189 + 76) y

29945 = (113) (265) y

y = 1

Using equation (i), we get

x = (189-37)/76

x = 152/76 = 2

 

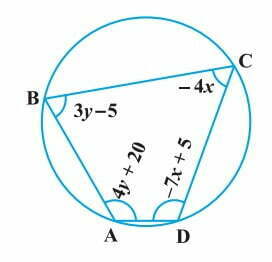
8. ABCD is a cyclic quadrilateral (see Fig. 3.7). Find the angles of the cyclic quadrilateral.

It is known that the sum of the opposite angles of a cyclic quadrilateral is 180^o

Thus, we have

∠C +∠A = 180

4y + 20− 4x = 180

− 4x + 4y = 160

x − y = − 40 …..(i)

And, ∠B + ∠D = 180

3y − 5 − 7x + 5 = 180

− 7x + 3y = 180 …..(ii)

Multiplying 3 to equation (i), we get

3x − 3y = − 120 ………(iii)

Adding equation (ii) to equation (iii), we get

− 7x + 3x = 180 – 120

− 4x = 60

x = −15

Substituting this value in equation (i), we get

x − y = − 40

-y−15 = − 40

y = 40-15

= 25

∠A = 4y + 20 = 20+4(25) = 120°

∠B = 3y − 5 = − 5+3(25) = 70°

∠C = − 4x = − 4(− 15) = 60°

∠D = 5-7x

∠D= 5− 7(−15) = 110°

Hence, all the angles are measured.