NCERT Solutions for Class 7 Maths
Chapter 5 Lines and Angles
Exercise 5.2
1. State the property that is used in each of the following statements?
(i) If a || b, then ∠1 = ∠5.
(ii) If ∠4 = ∠6, then a || b.
(iii) If ∠4 + ∠5 = 180°, then a || b.
Answer
(i) Corresponding angles property is used in the above statement.
(ii) Alternate interior angles property is used in the above statement.
(iii) Interior angles on the same side of transversal are supplementary.
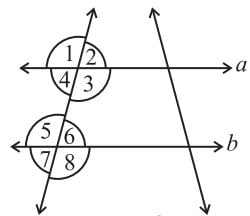
2. In the adjoining figure, identify
(i) the pairs of corresponding angles.
(ii) the pairs of alternate interior angles.
(iii) the pairs of interior angles on the same side of the transversal.
(iv) the vertically opposite angles.
Answer
By observing the figure, the pairs of corresponding angle are,
∠1 and ∠5, ∠4 and ∠8, ∠2 and ∠6, ∠3 and ∠7
(ii)By observing the figure, the pairs of alternate interior angle are,
∠2 and ∠8, ∠3 and ∠5
(iii) By observing the figure, the pairs of interior angles on the same side of the transversal are ∠2 and ∠5, ∠3 and ∠8
(iv) By observing the figure, the vertically opposite angles are,
∠1 and ∠3, ∠5 and ∠7, ∠2 and ∠4, ∠6 and ∠8
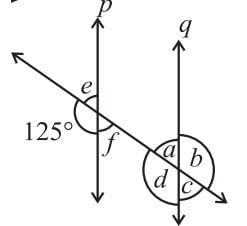
3. In the adjoining figure, p || q. Find the unknown angles.
Answer
By observing the figure,
∠d = ∠125o … [∵ corresponding angles]
We know that, Linear pair is the sum of adjacent angles is 180o
Then,
= ∠e + 125o = 180o … [Linear pair]
= ∠e = 180o – 125o
= ∠e = 55o
From the rule of vertically opposite angles,
∠f = ∠e = 55o
∠b = ∠d = 125o
By the property of corresponding angles,
∠c = ∠f = 55o
∠a = ∠e = 55o
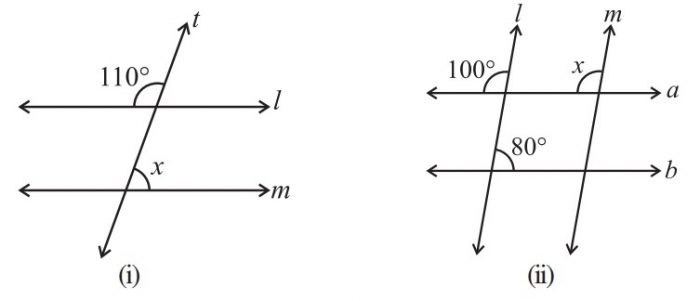
4. Find the value of x in each of the following figures if l || m.
Answer
(i) Let us assume other angle on the line m be ∠y,
Then,
By the property of corresponding angles,
∠y = 110o
We know that Linear pair is the sum of adjacent angles is 180o
Then,
= ∠x + ∠y = 180o
= ∠x + 110o = 180o
= ∠x = 180o – 110o
= ∠x = 70o
(ii) By the property of corresponding angles,
∠x = 100o
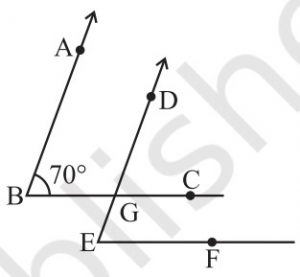
5. In the given figure, the arms of two angles are parallel.
If ∠ABC = 70º, then find
(i) ∠DGC
(ii) ∠DEF
Answer
(i) Let us consider that AB ∥ DG
BC is the transversal line intersecting AB and DG
By the property of corresponding angles,
∠DGC = ∠ABC
Then,
∠DGC = 70o
(ii) Let us consider that BC ∥ EF
DE is the transversal line intersecting BC and EF
By the property of corresponding angles,
∠DEF = ∠DGC
Then,
∠DEF = 70o
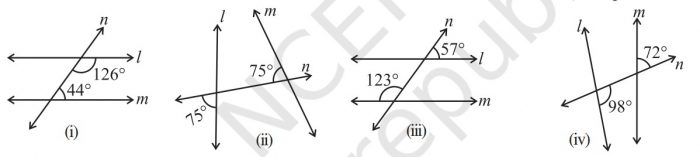
6. In the given figures below, decide whether l is parallel to m.
Answer
(i) Let us consider the two lines l and m,
n is the transversal line intersecting l and m.
We know that the sum of interior angles on the same side of transversal is 180o.|
Then,
= 126o + 44o
= 170o
But, the sum of interior angles on the same side of transversal is not equal to 180o.
So, line l is not parallel to line m.
(ii) Let us assume ∠x be the vertically opposite angle formed due to the intersection of the straight line l and transversal n,
Then, ∠x = 75o
Let us consider the two lines l and m,
n is the transversal line intersecting l and m.
We know that the sum of interior angles on the same side of transversal is 180o.
Then,
= 75o + 75o
= 150o
But, the sum of interior angles on the same side of transversal is not equal to 180o.
So, line l is not parallel to line m.
(iii) Let us assume ∠x be the vertically opposite angle formed due to the intersection of the Straight line l and transversal line n,
Let us consider the two lines l and m,
n is the transversal line intersecting l and m.
We know that the sum of interior angles on the same side of transversal is 180o.
Then,
= 123o + ∠x
= 123o + 57o
= 180o
∴ The sum of interior angles on the same side of transversal is equal to 180o.
So, line l is parallel to line m.
(iv) Let us assume ∠x be the angle formed due to the intersection of the Straight line l and transversal line n,
We know that Linear pair is the sum of adjacent angles is equal to 180o.
= ∠x + 98o = 180o
= ∠x = 180o – 98o
= ∠x = 82o
Now, we consider ∠x and 72o are the corresponding angles.
For l and m to be parallel to each other, corresponding angles should be equal.
But, in the given figure corresponding angles measures 82o and 72o respectively.
∴ Line l is not parallel to line m.
Leave a Reply