Miscellaneous Exercise
Binomial Theorem
Question and Answers
Class 11 – Maths
| Class | Class 11 |
| Subject | Mathematics |
| Chapter Name | Binomial Theorem |
| Chapter No. | Chapter 7 |
| Exercise | Miscellaneous Exercise |
| Category | Class 11 Maths NCERT Solutions |
Question 1 If a and b are distinct integers, prove that a – b is a factor of a n – b n , whenever n is a positive integer.
[Hint write an = (a – b + b) n and expand]
Answers
a = a − b + b
So, an = [a − b +b]n
= [(a − b) + b]n
= nC0 (a − b)n + nC1 (a − b)n−1b1 + nC2 (a − b)n−2b2 + …….+ nCn−1 (a − b)bn−1 + nCn (bn)
⇒ an − bn = (a − b)n + nC1 (a − b)n−1b + nC2 (a − b)n−2b2 + …….+ nCn−1 (a − b)bn−1
= (a − b) [(a − b)n−1 + nC1 (a − b)n−2b + nC2 (a − b)n−3b2 + ……+ nCn−1 bn−1]
= (a – b)[an integer]
⇒ an – bn is divisible by (a – b)
Question 2 Evaluate (√3 + √2)6 – ( √3 – √2 )6
Answers
= ((√3+ √2)2 − (√3−√2)2)3 + 3 (√3+√2)2( √3−√2)2 ((√3+√2)2−(√3+√2)2))
= (4√6)3 + 4√6(5+2√6) (5−2√6)
= 384√6+4√6
= 388√6
Question 3 Find the value of
Answers
Question 4 Find an approximation of (0.99)5 using the first three terms of its expansion
Answer 0.99 can be written as
0.99 = 1 – 0.01
Now, by applying the binomial theorem, we get
(o. 99)5 = (1 – 0.01)5
= 5C0 (1)5 – 5C1 (1)4 (0.01) + 5C2 (1)3 (0.01)2
= 1 – 5 (0.01) + 10 (0.01)2
= 1 – 0.05 + 0.001
= 0.951
Question 5 Expand using Binomial Theorem
Answer Using the binomial theorem, the given expression can be expanded as

Question 6 Find the expansion of (3x 2 – 2ax + 3a 2 ) 3 using binomial theorem.
(a + b)3 = a3 + 3a2b + 3ab2 + b3Putting a = 3x2
b = -a (2x-3a), we get
= (3x2)3+3(3x2)2(-a (2x-3a)) + 3(3x2) (-a (2x-3a))2 + (-a (2x-3a))3
= 27x6 – 27ax4 (2x-3a) + 9a2x2 (2x-3a)2 – a3(2x-3a)3
= 27x6 – 54ax5 + 81a2x4 + 9a2x2 (4x2-12ax+9a2) – a3 [(2x)3 – (3a)3 – 3(2x)2(3a) + 3(2x)(3a)2]
= 27x6 – 54ax5 + 81a2x4 + 36a2x4 – 108a3x3 + 81a4x2 – 8a3x3 + 27a6 + 36a4x2 – 54a5x
= 27x6 – 54ax5+ 117a2x4 – 116a3x3 + 117a4x2 – 54a5x + 27a6
Thus, (3x2 – 2ax + 3a2)3
= 27x6 – 54ax5+ 117a2x4 – 116a3x3 + 117a4x2 – 54a5x + 27a6
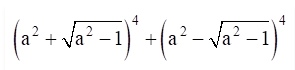


Leave a Reply