Miscellaneous Exercise
Permutations and combinations
Question and Answers
Class 11 – Maths
| Class | Class 11 |
| Subject | Mathematics |
| Chapter Name | Permutations and Combinations |
| Chapter No. | Chapter 6 |
| Exercise | Miscellaneous Exercise |
| Category | Class 11 Maths NCERT Solutions |
Question 1 How many words, with or without meaning, each of 2 vowels and 3 consonants can be formed from the letters of the word DAUGHTER ?
Answer
In the word DAUGHTER, there are 3 vowels namely, A, U, and E, and 5 consonants namely, D, G, H, T, and R.
Number of ways of selecting 2 vowels out of 3 vowels = 3C2 = 3
Number of ways of selecting 3 consonants out of 5 consonants = 5C3 = 10
Therefore, number of combinations of 2 vowels and 3 consonants = 3 × 10 = 30
Each of these 30 combinations of 2 vowels and 3 consonants can be arranged among themselves in 5! ways.
Hence, required number of different words = 30 × 5! = 3600
Question 2 How many words, with or without meaning, can be formed using all the letters of the word EQUATION at a time so that the vowels and consonants occur together?
Answer In the word EQUATION, there are 5 vowels, namely, A, E, I, O, and U, and 3 consonants, namely, Q, T, and N.
Since all the vowels and consonants have to occur together, both (AEIOU) and (QTN) can be assumed as single objects. Then, the permutations of these 2 objects taken all at a time are counted. This number would be 2C2 = 2!
Corresponding to each of these permutations, there are 5! permutations of the five vowels taken all at a time and 3! permutations of the 3 consonants taken all at a time.
Hence, by multiplication principle, required number of words = 2! × 5! × 3! = 1440
Question 3 A committee of 7 has to be formed from 9 boys and 4 girls. In how many ways can this be done when the committee consists of:
(i) exactly 3 girls ?
(i) Out of 9 boys and 4 girls, a committee of 7 has to be formed.
Exactly 3 girls should be there in a committee, hence, number of boys = (7 – 3) = 4 boys only.
Total ways of forming the committee with exactly three girls = 4C3 × 9C4
(ii) atleast 3 girls ?
Since at least 3 girls are to be there in every committee, the committee can consist of
(a) 3 girls and 4 boys or (b) 4 girls and 3 boys
3 girls and 4 boys can be selected in 4C3 × 9C4 ways.
4 girls and 3 boys can be selected in 4C3 × 9C4 ways.
Therefore, in this case, required number of ways = 4C3 × 9C4 + 4C3 × 9C4
= 504 + 84 = 588
(iii) atmost 3 girls ?
Since at most 3 girls are to be there in every committee, the committee can consist of
(a) 3 girls and 4 boys (b) 2 girls and 5 boys
(c) 1 girl and 6 boys (d) No girl and 7 boys
3 girls and 4 boys can be selected in 4C3 × 9C4 ways.
2 girls and 5 boys can be selected in 4C2 × 9C5 ways.
1 girl and 6 boys can be selected in 4C1 × 9C6 ways .
No girl and 7 boys can be selected in 4C0 × 9C7 ways .
Therefore, in this case, required number of ways .
The number of choosing 3 girls and 4 boys = 504
The total number of ways in which a committee can have at most 3 girls are = 36 + 336 + 756 + 504 = 1632
Question 4 If the different permutations of all the letter of the word EXAMINATION are listed as in a dictionary, how many words are there in this list before the first word starting with E ?
Answer There are a total of 11 letters out of which A, I and N appears 2 times and other letters appear only once.
The words starting with A will be the words listed before the words starting with E.
Thus, words starting with letter A will have letter A fixed at its extreme left end.
And remaining 10 letters are rearranged all at a time.
In the remaining 10 letters, there are 2 I’s and 2 N’s.
Question 5 How many 6-digit numbers can be formed from the digits 0, 1, 3, 5, 7 and 9 which are divisible by 10 and no digit is repeated ?
Answer The number is divisible by 10 if the unit place has 0 in it.Therefore, 0 is fixed at the units place.
The 6-digit number is to be formed
Therefore, the 5 vacant places can be filled by remaining 5 digits.
These 5 empty places can be filled in 5! ways.
Therefore, number of 6-digit numbers = 5! = 120.
Question 6 The English alphabet has 5 vowels and 21 consonants. How many words with two different vowels and 2 different consonants can be formed from the alphabet ?
Answer We know that there are 5 vowels and 21 consonants in the English alphabet.
Choosing two vowels out of 5 would be done in 5C2 ways.
Choosing 2 consonants out of 21 can be done in 21C2 ways.
The total number of ways to select 2 vowels and 2 consonants = 5C2 × 21C2
Every 2100 combination consists of 4 letters, which can be arranged in 4! ways.
Therefore, number of words = 2100 × 4! = 50400
Question 7 In an examination, a question paper consists of 12 questions divided into two parts i.e., Part I and Part II, containing 5 and 7 questions, respectively. A student is required to attempt 8 questions in all, selecting at least 3 from each part. In how many ways can a student select the questions?
Answer It is given that the question paper consists of 12 questions divided into two parts – Part I and Part II, containing 5 and 7 questions, respectively.
A student has to attempt 8 questions, selecting at least 3 from each part.
This can be done as follows.
(a) 3 questions from part I and 5 questions from part II
(b) 4 questions from part I and 4 questions from part II
(c) 5 questions from part I and 3 questions from part II
3 questions from part I and 5 questions from part II can be selected in 5C3 × 7C5 ways.
4 questions from part I and 4 questions from part II can be selected in 5C4 × 7C4 ways.
5 questions from part I and 3 questions from part II can be selected in 5C5 × 7C3 ways.
Now the total number of ways in which a student can choose the questions are
210 +175 +35 = 420
Question 8 Determine the number of 5-card combinations out of a deck of 52 cards if each selection of 5 cards has exactly one king.
Answer We have a deck of cards that has 4 kings.
The numbers of remaining cards are 52.
Ways of selecting a king from the deck = 4C1
Ways of selecting the remaining 4 cards from 48 cards= 48C4
The total number of selecting the 5 cards having one king always = 4C1 × 48C4
Question 9 It is required to seat 5 men and 4 women in a row so that the women occupy the even places. How many such arrangements are possible ?
Answer 5 men and 4 women should be seated so that women always occupy the even places.
Women occupy even places, which means they will be sitting in 2nd, 4th, 6th and 8th places, whereas men will be sitting in 1st, 3rd, 5th,7th and 9th places.
4 women can sit in four places and ways they can be seated= 4P4 = 24
5 men can occupy 5 seats in 5 ways and the number of ways in which these can be seated = 5P5 = 120
The total number of sitting arrangements possible = 24 × 120 = 2880
Question 10 From a class of 25 students, 10 are to be chosen for an excursion party. There are 3 students who decide that either all of them will join or none of them will join. In how many ways can the excursion party be chosen ?
Answer From the class of 25 students, 10 are to be chosen for an excursion party.
Since there are 3 students who decide that either all of them will join or none of them will join, there are two cases.
(i) Either all 3 will go
The remaining students in the class are: 25 – 3 = 22
The number of students that remain to be chosen for the party = 7
The number of ways to choose the remaining 22 students = 22C7 = 170544
(ii) None of them will go.
The students going will be 10.
Remaining students eligible for going = 22
The number of ways in which these 10 students can be selected is 22C10 = 646646
The total number of ways in which students can be chosen = 170544 + 646646 = 817190
Question 11 In how many ways can the letters of the word ASSASSINATION be arranged so that all the S’s are together?
Answer In the given word ASSASSINATION, the letter A appears 3 times, S appears 4 times, I appears 2 times, N appears 2 times, and all the other letters appear only once.
Since all the words have to be arranged in such a way that all the S are together, SSSS is treated as a single object for the time being. This single object together with the remaining 9 objects will account for 10 objects.
These 10 objects in which there are 3 As, 2 Is, and 2 Ns can be arranged in
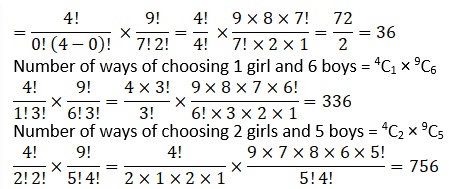
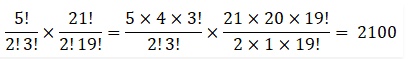
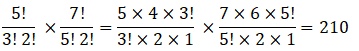
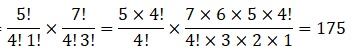
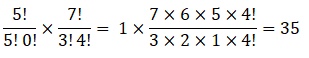
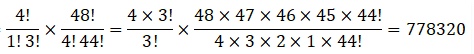
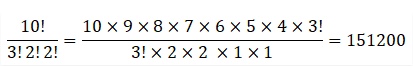
Leave a Reply