Miscellaneous Exercise
Linear Equations
Question and Answers
Class 11 – Maths
| Class | Class 11 |
| Subject | Mathematics |
| Chapter Name | Linear Equations |
| Chapter No. | Chapter 5 |
| Exercise | Miscellaneous Exercise |
| Category | Class 11 Maths NCERT Solutions |
Question 1 Solve the inequality 2 ≤ 3x – 4 ≤ 5
Answer The inequality given is
2 ≤ 3x – 4 ≤ 5
⇒ 2 ≤ 3x – 4 ≤ 5
⇒ 2 + 4 ≤ 3x – 4 + 4 ≤ 5 + 4
⇒ 6 ≤ 3x ≤ 9
⇒ 6/3 ≤ 3x/3 ≤ 9/3
⇒ 2 ≤ x ≤ 3
Hence, all real numbers x greater than or equal to 2 but less than or equal to 3 are solutions of given equality.
x ∈ [2, 3]
Question 2 Solve the inequality : 6 ≤ – 3 (2x – 4) < 12
Answer The inequality given is
6 ≤ –3 (2x – 4) < 12
⇒ 6 ≤ -3 (2x – 4) < 12
Dividing the inequality by 3, we get
⇒ 2 ≤ – (2x – 4) < 4
Multiplying the inequality by -1,
⇒ -2 ≥ 2x – 4 > -4 [multiplying the inequality with -1 changes the inequality sign.]
⇒ -2 + 4 ≥ 2x – 4 + 4 > -4 + 4
⇒ 2 ≥ 2x > 0
Dividing the inequality by 2,
⇒ 0 < x ≤ 1
Hence, all real numbers x greater than 0 but less than or equal to 1 are solutions of given equality.
x ∈ (0, 1]
Question 3 Solve the inequality : – 3 ≤ 4 – 7x/2 ≤ 18
Answer
– 3 ≤ 4 – 7x/2 ≤ 18
As a result, the set of solutions for the given inequality is [−4,2].
Question 4 Solve the inequality :
Answer 4) The inequality given is
– 15 ≤ 3(x – 2)/5 ≤ 0
⇒ – 15 < 3(x – 2)/5 ≤ 0
Multiplying the inequality by 5,
-75 < 3(x – 2) ≤ 0
Dividing the inequality by 3, we get
⇒ -25 < x – 2 ≤ 0
⇒ – 25 + 2 < x – 2 + 2 ≤ 0 + 2
⇒ – 23 < x ≤ 2
Hence, all real numbers x greater than -23 but less than or equal to 2 are solutions of given equality.
x ∈ (-23, 2]
Question 5 Solve the inequality :
Answer
Question 6 Solve the inequality :
Answer 6)
All real numbers x greater than or equal to -4 but less than or equal to 2 are solutions of given equality.
x ∈ [1, 11/3]
Question 7 Solve the inequalities and represent the solution graphically on number line: 5x + 1 > – 24, 5x – 1 < 24
Answer 5x + 1 > -24 and 5x – 1 < 24
5x + 1 > -24
⇒ 5x > -24 – 1
⇒ 5x > -25
⇒ x > -5 ……… (i)
5x – 1 < 24
⇒ 5x < 24 + 1
⇒ 5x < 25
⇒ x < 5 ……….(ii)
From equations (i) and (ii),
We can infer that the solution of given inequalities is (-5, 5).
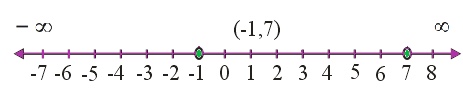
Question 8 Solve the inequalities and represent the solution graphically on number line:
2 (x – 1) < x + 5, 3 (x + 2) > 2 – x
Answer
2 (x – 1) < x + 5 and 3 (x + 2) > 2 – x
2 (x – 1) < x + 5
⇒ 2x – 2 < x + 5
⇒ 2x – x < 5 + 2
⇒ x < 7 ……… (i)
3 (x + 2) > 2 – x
⇒ 3x + 6 > 2 – x
⇒ 3x + x > 2 – 6
⇒ 4x > -4
⇒ x > -1 ………. (ii)
From equations (i) and (ii),
We can infer that the solution of given inequalities is (-1, 7).
Question 9 Solve the inequalities and represent the solution graphically on number line: 3x – 7 > 2 (x – 6) , 6 – x > 11 – 2x
Answer
3x – 7 > 2(x – 6) and 6 – x > 11 – 2x
3x – 7 > 2(x – 6)
⇒ 3x – 7 > 2x – 12
⇒ 3x – 2x > 7 – 12
⇒ x > -5 ………… (i)
6 – x > 11 – 2x
⇒ 2x – x > 11 – 6
⇒ x > 5 ……….(ii)
From equations (i) and (ii),
We can infer that the solution of given inequalities is (5, ∞).
Question 10 Solve the inequalities and represent the solution graphically on number line: 5(2x – 7) – 3(2x + 3) ≤ 0, 2x + 19 ≤ 6x + 47
Answer 5(2x – 7) – 3(2x + 3) ≤ 0 and 2x + 19 ≤ 6x + 47
5(2x – 7) – 3(2x + 3) ≤ 0
⇒ 10x – 35 – 6x – 9 ≤ 0
⇒ 4x – 44 ≤ 0
⇒ 4x ≤ 44
⇒ x ≤ 11 ……(i)
2x + 19 ≤ 6x +47
⇒ 6x – 2x ≥ 19 – 47
⇒ 4x ≥ -28
⇒ x ≥ -7 ……….(ii)
From equations (i) and (ii),
We can infer that the solution of given inequalities is (-7, 11).
Question 11 A solution is to be kept between 68° F and 77° F. What is the range in temperature in degree Celsius (C) if the Celsius / Fahrenheit (F) conversion formula is given by F = (9/5) C + 32?
Answer The solution has to be kept between 68° F and 77° F. So, we get 68° < F < 77°
The required temperature range in degrees Celsius is between 20° C to 25° C.
Question 12 A solution of 8% boric acid is to be diluted by adding a 2% boric acid solution to it. The resulting mixture is to be more than 4% but less than 6% boric acid. If we have 640 litres of the 8% solution, how many litres of the 2% solution will have to be added?
Answer 8% of solution of boric acid = 640 litres
Let the amount of 2% boric acid solution added = x litres
Total mixture = x + 640 litres
The resulting mixture has to be more than 4% but less than 6% boric acid.
∴ 2% of x + 8% of 640 > 4% of (x + 640) and
2% of x + 8% of 640 < 6% of (x + 640)
2% of x + 8% of 640 > 4% of (x + 640)
⇒ (2/100) × x + (8/100) × 640 > (4/100) × (x + 640)
⇒ 2x + 5120 > 4x + 2560
⇒ 5120 – 2560 > 4x – 2x
⇒ 2560 > 2x
⇒ x < 1280 ….(i)
2% of x + 8% of 640 < 6% of (x + 640)
⇒ (2/100) × x + (8/100) × 640 < (6/100) × (x + 640)
⇒ 2x + 5120 < 6x + 3840
⇒ 6x – 2x > 5120 – 3840
⇒ 4x > 1280
⇒ x > 320 ……….(i)
From (i) and (ii),
320 < x < 1280
Therefore, the number of litres of 2% of boric acid solution that has to be added will be more than 320 litres but less than 1280 litres.
Question 13 How many litres of water will have to be added to 1125 litres of the 45% solution of acid so that the resulting mixture will contain more than 25% but less than 30% acid content?
Answer 45% of solution of acid = 1125 litres
Let the amount of water added = x litres
Resulting mixture = x + 1125 litres
The resulting mixture has to be more than 25% but less than 30% acid content.
Amount of acid in the resulting mixture = 45% of 1125 litres
∴ 45% of 1125 < 30% of (x + 1125) and 45% of 1125 > 25% of (x + 1125)
45% of 1125 < 30% of (x + 1125)
45% of 1125 < 30% of (x + 1125)
⇒ 45 × 1125 < 30x + 30 × 1125
⇒ (45 – 30) × 1125 < 30x
⇒ 15 × 1125 < 30x
⇒ x > 562.5 ………..(i)
45% of 1125 > 25% of (x + 1125)
⇒ 45 × 1125 > 25x + 25 × 1125
⇒ (45 – 25) × 1125 > 25x
⇒ 25x < 20 × 1125
⇒ x < 900 …..(ii)
∴ 562.5 < x < 900
Therefore, the number of litres of water that has to be added will have to be more than 562.5 litres but less than 900 litres.
Question 14 IQ of a person is given by the formula, IQ = (MA/CA ) × 100, where MA is mental age and CA is chronological age. If 80 ≤ IQ ≤ 140 for a group of 12 years old children, find the range of their mental age.
Answer Chronological age = CA = 12 years
IQ for the age group of 12 is 80 ≤ IQ ≤ 140.
We get that
80 ≤ IQ ≤ 140
Substituting,
⇒ 9.6 ≤ MA ≤ 16.8
∴ The range of mental age of the group of 12 years old children is 9.6 ≤ MA ≤ 16.8
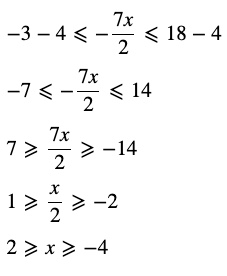
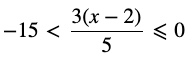
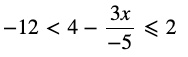
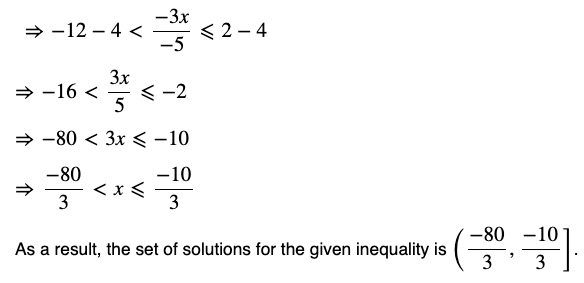
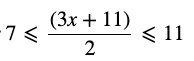
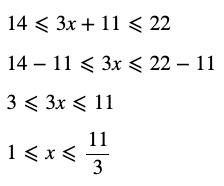
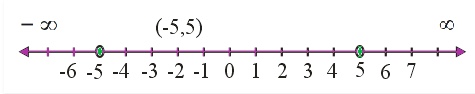
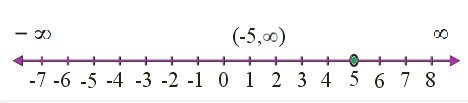
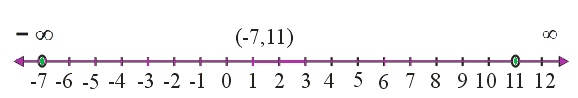
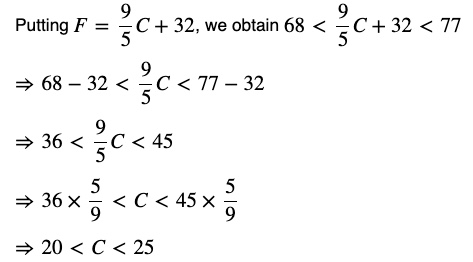



Leave a Reply