Miscellaneous Exercise
Complex Numbers and Quadratic Numbers
Question and Answers
Class 11 – Maths
| Class | Class 11 |
| Subject | Mathematics |
| Chapter Name | Complex Numbers and Quadratic Numbers |
| Chapter No. | Chapter 4 |
| Exercise | Miscellaneous Exercise |
| Category | Class 11 Maths NCERT Solutions |
Question 1 Evaluate
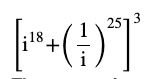
Answer
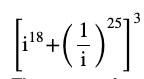
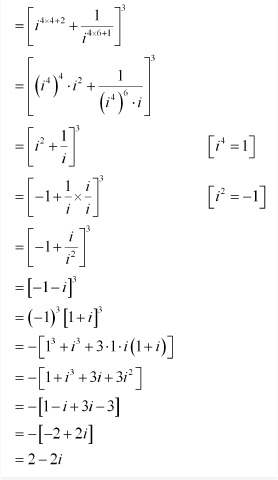
Question 2 For any two complex numbers z 1 and z 2, prove that
Re (z1z2) = Re z1 Re z2 – Im z1 Im z2
Answer
Let Let z1=x1+iy1 and z2=x2+iy2
Product of these two complex numbers, z1 z2
z1 z2 = ( x1+iy1 ) (x2+iy2)
z1 z2 = x1 (x2+iy2) + iy1 (x2+iy2)
z1 z2 = x1x2+ix1y2+iy1x2+i2y1y2
z1 z2 = x1x2+ix1y2+iy1x2−y1y2
z1 z2 = (x1x2−y1y2)+i(x1y2+y1x2)
Re(z1z2)=x1x2−y1y2
Re (z1z2) = Re z1 Re z2 – Im z1 Im z2
Question 3 Reduce to the standard form
Answer
Question 4
Answer
Question 5 If z 1 = 2 – i, z 2 = 1 + i, find
Answer
Question 6
Answer
Question 7 Let z1 = 2 – i, z2 = –2 + i. Find
(i)
z1 = 2 – i, z2 = –2 + i
z1 z2 = (2-i) (-2 +1)
z1 z2= −4+2i+2i−i2
z1 z2 = −4+4i−(−1)
z1 z2= -3 + 4i
(ii)
Question 8 Find the real numbers x and y if (x – iy) (3 + 5i) is the conjugate of –6 – 24i
Answer
z = (x – iy) (3 + 5i)
z = 3x + 5 xi− 3 yi− 5yi2
z = 3x + 5xi − 3yi + 5y
z = (3x+5y) + i (5x−3y)
z̅ = − 6 − 24i
(3x+5y) + i (5x−3y) = − 6 − 24i
On equating real and imaginary parts, we have
3x + 5y = -6 …… (i)
5x – 3y = 24 …… (ii)
Performing (i) x 3 + (ii) x 5, we get
(9x + 15y) + (25x – 15y) = -18 + 120
34x = 102
x = 102/34 = 3
Putting the value of x in equation (i), we get
3(3) + 5y = -6
5y = -6 – 9 = -15
y = -3
Therefore, the values of x and y are 3 and –3 respectively.
Question 9 Find the modulus of
Answer
Question 10 If (x + iy)3 = u + iv, then show that
Answer
(x + iy)3 = u +iv
x3 + (iy)3+ 3 × x × iy (x+iy) = u+iv
x3 + i3y3 + 3x2yi + 3xy2i2 = u+iv
x3−iy3+3x2yi−3xy2=u+iv
(x3−3xy2)+i(3x2y−y3)=u+iv
On equating real and imaginary
u=x3−3xy2 ,v=3x2y−y3
= x2−3y2+3x2−y2
=4x2 -4y2
=4 (x2– y2)
Question 11 If α and β are different complex numbers with |β| = 1, then find
Answer
Let α = a + ib and β = x +iy
|β|= 1
Question 12) Find the number of non-zero integral solutions of the equation |1 – i|x = 2x
Answer
|1 – i|x = 2x
2x/2 = 2x
x/2 = x
x = 2x
2x – x = 0
x = 0
Thus, 0 is the only integral solution of the given equation. Therefore, the number of non- zero integral solutions of the given equation is 0.
Question 13 If (a + ib)(c + id)(e + if)(g + ih) = A + iB, then show that
(a2 + b2)(c2 + d2)(e2 + f2 )(g2 + h2) = A2 + B2.
Answer
(a + ib)(c + id)(e + if)(g + ih) = A + iB
∴ |(a + ib)(c + id)(e + if)(g + ih)| = |A + iB|
⇒ |(a + ib)|× |(c + id)|× |(e + if)| × |(g + ih)| = |A + B| [|z1 z2| z1||z2|]
On squaring both sides, we obtain
(a2 + b2 )(c2 + d2 )(e2 + f2 )(g2 + h2 ) = A2 + B2 .
Hence, proved.
Question 14 If [(1 +i)/(1 – i)]m = 1, then find the least positive integral value of m.
Answer
im =1
im= i4k
m=4k where k is some integer. Therefore, the least positive is one. Thus, the least positive integral value of m is 4=( 4× 1)



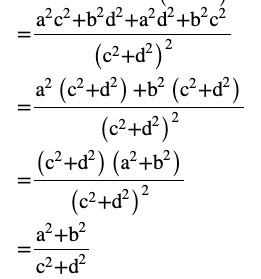
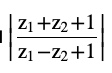
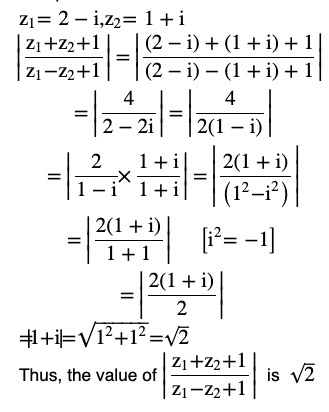

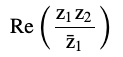
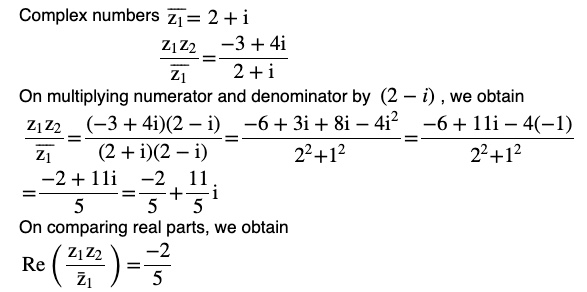

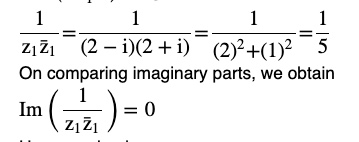
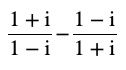
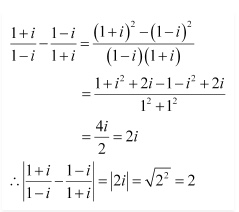
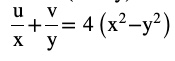
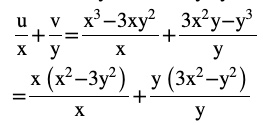

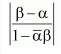
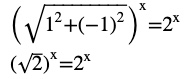
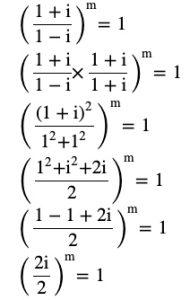
Leave a Reply