Miscellaneous Exercise
Trigonometric Functions
Question and Answers
Class 11 – Maths
| Class | Class 11 |
| Subject | Mathematics |
| Chapter Name | Trigonometric Functions |
| Chapter No. | Chapter 3 |
| Exercise | Miscellaneous Exercise |
| Category | Class 11 Maths NCERT Solutions |
Question (1) Prove that
Answer
Question (2) Prove that (sin 3x + sin x) sin x + (cos 3x – cos x) cos x = 0
Answer
LHS = (sin 3x + sin x) sin x + (cos 3x – cos x) cos x
LHS = sin 3x sin x + sin2 x + cos 3x cos x – cos2 x
Taking out the common terms,
LHS = cos 3x cos x + sin 3x sin x – (cos2 x – sin2 x)
Using the formula
cos (A – B) = cos A cos B + sin A sin B
= cos (3x – x) – cos 2x
So, we get
= cos 2x – cos 2x
= 0
= RHS
Question (3) Prove that
Answer
cos(x+y)=cos x cos y-sin x sin y
L.H.S=(cos x + cos y)2+(sin x – sin y)2
By expanding using the formula, we get
LHS = cos2 x + cos2 y + 2 cos x cos y + sin2 x + sin2 y – 2 sin x sin y
Grouping the terms,
= (cos2 x + sin2 x) + (cos2 y + sin2 y) + 2 (cos x cos y – sin x sin y)
Using the formula cos (A + B) = (cos A cos B – sin A sin B)
= 1 + 1 + 2 cos (x + y)
By further calculation,
= 2 + 2 cos (x + y)
Taking 2 as common
= 2 [1 + cos (x + y)]
From the formula cos 2A = 2 cos2 A – 1
Therefore , LHS =RHS
Hence Proved
Question (4) Prove that
Answer
LHS = (cos x – cos y) 2 + (sin x – sin y) 2
By expanding using the formula,
= cos2 x + cos2 y – 2 cos x cos y + sin2 x + sin2 y – 2 sin x sin y
Grouping the terms,
= (cos2 x + sin2 x) + (cos2 y + sin2 y) – 2 (cos x cos y + sin x sin y)
Using the formula cos (A – B) = cos A cos B + sin A sin B
= 1 + 1 – 2 [cos (x – y)]
By further calculation,
= 2 [1 – cos (x – y)]
From formula cos 2A = 1 – 2 sin2 A
LHS =RHS
Hence proved
Question (5) Prove that sin x + sin 3x + sin 5x + sin 7x = 4 cos x cos 2x sin 4x
Answer
L.H.S. =sin x + sin 3x+sin 5x+sin 7x
LHS=(sin x + sin 5x)+(sin 3x+sin 7x)
LHS =(sin x + sin 5x)+(sin 3x+sin 7x)
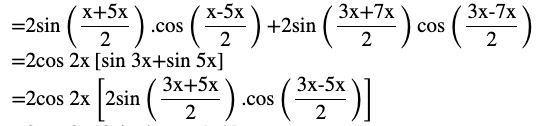
L.H.S = 4 cos 2x sin 4x cos x = R.H.S
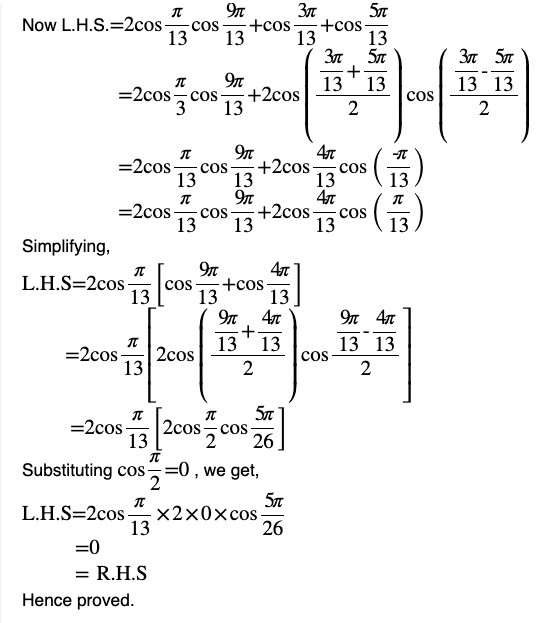
Question (6) Prove that
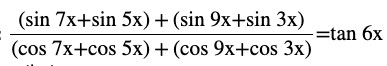
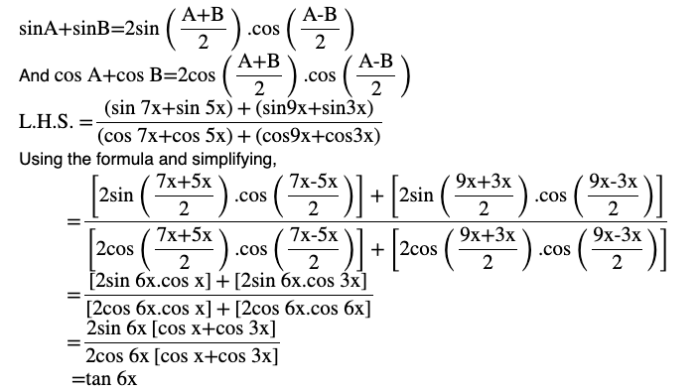
Therefore L.H.S = R.H.SQuestion (7) Prove that sin 3x + sin 2x – sin x = 4 sin x cos ( x /2) cos (3x /2)Answer
Question (8) Find
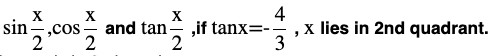
Here, x is in 2nd quadrant.
π / 2 < x < π
Dividing by 2
π / 4 < x/2 < π /2
Hence x/2 lies in the 1st quadrant
Therefore , sin x/2 , cos x/2 and tan x/2 are positive
Given that tan = -4/3
sec2x=1+tan2x
sec2x=1+ (-4/3)2
sec2x=1+ (16/9)
sec2x= 25/9
sec x = ± 5/3
As x is in 2nd quadrant, sec x is negative.
sec x = – 5/3
Then cos x= -3/5
2Cos2 x/2 = cos x + 1
2Cos2 x/2 = 2/5
Cos x/2 = 1/ √5 = √5 / 5
sin2x/ 2 + cos2x/2 =1
Sin2 x/2 + ( 1/ √5 )2 =1
Sin2 x/2 = 4/5
Sin x/2 = 2 / √5
Sin x/2 = 2 √5 / 5
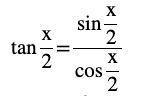
Sin x/2, cos x/2, and tan x/2 are 2√5 / 5, √5 / 5, 2
Question (9) Find
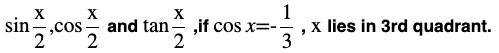
Answer
π < x < 3 π / 2
The values of sin x/2 , cos x/2 and tan x/2 are √2/ √3 , -1/3 , – √2Question (10) Find
x lies in 2nd quadrant
π /2 < x < π
Dividing by 2
π / 4 < x/2 < π /2
X/2 lies in the 1st quadrant therefore sin x/2, cos x/2, and tan x/2 are positive.
sin x =1/4
sin2x+cos2x=1
cos2 x = 1 – sin2x
cos2 x = 1 – (1/4)2
cos2 x = 15/16
cos x= – √15 /4
2 sin2 x/2 = 1 – cos x/ 2
2 sin2 x/2 = 1 + √15 /4

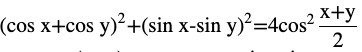
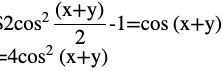
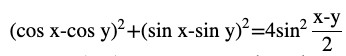
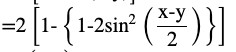
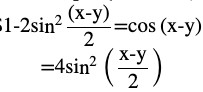
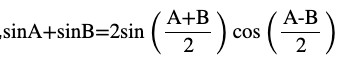

Leave a Reply