Exercise 7.1
Binomial Theorem
Question and Answers
Class 11 – Maths
| Class | Class 11 |
| Subject | Mathematics |
| Chapter Name | Binomial Theorem |
| Chapter No. | Chapter 7 |
| Exercise | Exercise 7.1 |
| Category | Class 11 Maths NCERT Solutions |
Expand each of the expressions in Exercises 1 to 5.
(1) (1–2x) 5
(1 – 2x)5 = 5Co (1)5 – 5C1 (1)4 (2x) + 5C2 (1)3 (2x)2 – 5C3 (1)2 (2x)3 + 5C4 (1)1 (2x)4 – 5C5 (2x)5
= 1 – 5 (2x) + 10 (4x)2 – 10 (8x3) + 5 ( 16 x4) – (32 x5)
= 1 – 10x + 40x2 – 80x3 + 80x4– 32x5
(2)
(3) (2x – 3)6
=6C0(2x)6 − 6C1(2x)5(3) + 6C2(2x)4(3)2 − 6C3(2x)3(3)3 + 6C4(2x)2(3)4 − 6C5(2x(3)5 + 6C6(3)6
=64x6 − 6(32x5)(3) + 15(16x4)(9) − 20(8X3)(27) + 15(4x2)(81) − 6(2x)(243) + 729
=64x6 − 576x5 + 2160x4− 4320x3 + 4860x2 − 2916 x + 729
(4)
(5)
Using binomial theorem, evaluate each of the following:
(6) (96)3
Answer
The given question can be written as 96 = 100 – 4
(96)3 = (100 – 4)3
= 3C0 (100)3 – 3C1 (100)2 (4) – 3C2 (100) (4)2– 3C3 (4)3
= (100)3 – 3 (100)2 (4) + 3 (100) (4)2 – (4)3
= 1000000 – 120000 + 4800 – 64
= 884736
(7) (102)5
Answer
The given question can be written as 102 = 100 + 2
(102)5 = (100 + 2)5
= 5C0 (100)5 + 5C1 (100)4 (2) + 5C2 (100)3 (2)2 + 5C3 (100)2 (2)3 + 5C4 (100) (2)4 + 5C5 (2)5
= (100)5 + 5 (100)4 (2) + 10 (100)3 (2)2 + 5 (100) (2)3 + 5 (100) (2)4 + (2)5
= 1000000000 + 1000000000 + 40000000 + 80000 + 8000 + 32
= 11040808032
(8) (101)4
Answer
The given question can be written as 101 = 100 + 1
(101)4 = (100 + 1)4
= 4C0 (100)4 + 4C1 (100)3 (1) + 4C2 (100)2 (1)2 + 4C3 (100) (1)3 + 4C4 (1)4
= (100)4 + 4 (100)3 + 6 (100)2 + 4 (100) + (1)4
= 100000000 + 400000 + 60000 + 400 + 1
= 104060401
(9) (99)5
Answer
The given question can be written as 99 = 100 -1
(99)5 = (100 – 1)5
= 5C0 (100)5 – 5C1 (100)4 (1) + 5C2 (100)3 (1)2 – 5C3 (100)2 (1)3 + 5C4 (100) (1)4 – 5C5 (1)5
= (100)5 – 5 (100)4 + 10 (100)3 – 10 (100)2 + 5 (100) – 1
= 1000000000 – 5000000000 + 10000000 – 100000 + 500 – 1
= 9509900499
(10) Using Binomial Theorem, indicate which number is larger (1.1)10000 or 1000.
Answer
By splitting the given 1.1 and then applying the binomial theorem,
the first few terms of (1.1)10000 can be obtained as
(1.1)10000 = (1 + 0.1)10000
= (1 + 0.1)10000 C1 (1.1) + other positive terms
= 1 + 10000 × 1.1 + other positive terms
= 1 + 11000 + other positive terms
> 1000
(1.1)10000 > 1000
(11) Find (a+b)4 – (a-b)4. Evaluate
Answer
Using the binomial theorem, the expression (a + b)4 and (a – b)4 can be expanded
(a + b)4 = 4C0 a4 + 4C1 a3 b + 4C2 a2 b2 + 4C3 a b3 + 4C4 b4
(a – b)4 = 4C0 a4 – 4C1 a3 b + 4C2 a2 b2 – 4C3 a b3 + 4C4 b4
Now, (a + b)4 – (a – b)4 = 4C0 a4 + 4C1 a3 b + 4C2 a2 b2 + 4C3 a b3 + 4C4 b4 – [4C0 a4 – 4C1 a3 b + 4C2 a2 b2 – 4C3 a b3 + 4C4 b4]
= 2 (4C1 a3 b + 4C3 a b3)
= 2 (4a3 b + 4ab3)
= 8ab (a2 + b2)
Now, by substituting a = √3 and b = √2, we get
(√3 + √2)4 – (√3 – √2)4 = 8 (√3) (√2) {(√3)2 + (√2)2}
= 8 (√6) (3 + 2)
= 40 √6
(12) Using the binomial theorem, the expressions (x + 1)6 and (x – 1)6 can be expressed as
Answer
(x + 1)6 = 6C0 x6 + 6C1 x5 + 6C2 x4 + 6C3 x3 + 6C4 x2 + 6C5 x + 6C6
(x – 1)6 = 6C0 x6 – 6C1 x5 + 6C2 x4 – 6C3 x3 + 6C4 x2 – 6C5 x + 6C6
Now, (x + 1)6 – (x – 1)6 = 6C0 x6 + 6C1 x5 + 6C2 x4 + 6C3 x3 + 6C4 x2 + 6C5 x + 6C6
– [6C0 x6 – 6C1 x5 + 6C2 x4 – 6C3 x3 + 6C4 x2 – 6C5 x + 6C6]
= 2 [6C0 x6 + 6C2 x4 + 6C4 x2 + 6C6]
= 2 [x6 + 15x4 + 15x2 + 1]
Now, by substituting x = √2, we get
(√2 + 1)6 – (√2 – 1)6 = 2 [(√2)6 + 15(√2)4 + 15(√2)2 + 1]
= 2 (8 + 15 × 4 + 15 × 2 + 1)
= 2 (8 + 60 + 30 + 1)
= 2 (99)
= 198
(13) Find (x + 1)6 + (x – 1)6. Hence, or otherwise, evaluate
Answer
(x + 1)6 = 6C0 x6 + 6C1 x5 + 6C2 x4 + 6C3 x3 + 6C4 x2 + 6C5 x + 6C6
(x – 1)6 = 6C0 x6 – 6C1 x5 + 6C2 x4 – 6C3 x3 + 6C4 x2 – 6C5 x + 6C6
Now, (x + 1)6 – (x – 1)6 = 6C0 x6 + 6C1 x5 + 6C2 x4 + 6C3 x3 + 6C4 x2 + 6C5 x + 6C6
– [6C0 x6 – 6C1 x5 + 6C2 x4 – 6C3 x3 + 6C4 x2 – 6C5 x + 6C6]
= 2 [6C0 x6 + 6C2 x4 + 6C4 x2 + 6C6]
= 2 [x6 + 15x4 + 15x2 + 1]
Now, by substituting x = √2, we get
(√2 + 1)6 – (√2 – 1)6 = 2 [(√2)6 + 15(√2)4 + 15(√2)2 + 1]
= 2 (8 + 15 × 4 + 15 × 2 + 1)
= 2 (8 + 60 + 30 + 1)
= 2 (99)
= 198
(14) Show that 9n+1 – 8n – 9 is divisible by 64, whenever n is a positive integer.
Answer
In order to show that 9n+1 – 8n – 9 is divisible by 64, it has to be shown that 9n+1 – 8n – 9 = 64 k,
where k is some natural number
Using the binomial theorem,
(1 + a)m = mC0 + mC1 a + mC2 a2 + …. + m C m am
For a = 8 and m = n + 1, we get
(1 + 8)n+1 = n+1C0 + n+1C1 (8) + n+1C2 (8)2 + …. + n+1 C n+1 (8)n+1
9n+1 = 1 + (n + 1) 8 + 82 [n+1C2 + n+1C3 (8) + …. + n+1 C n+1 (8)n-1]
9n+1 = 9 + 8n + 64 [n+1C2 + n+1C3 (8) + …. + n+1 C n+1 (8)n-1]
9n+1 – 8n – 9 = 64 k
Where k = [n+1C2 + n+1C3 (8) + …. + n+1 C n+1 (8)n-1] is a natural number
Thus, 9n+1 – 8n – 9 is divisible by 64 whenever n is a positive integer.
Hence, the proof.
(15) Prove that
Answer
15)
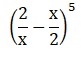
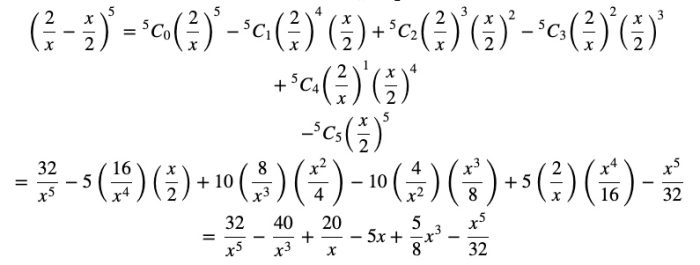
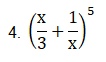
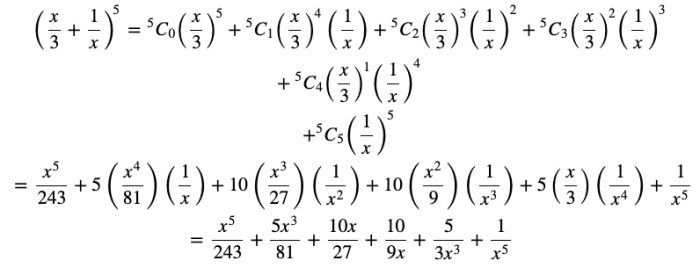
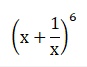
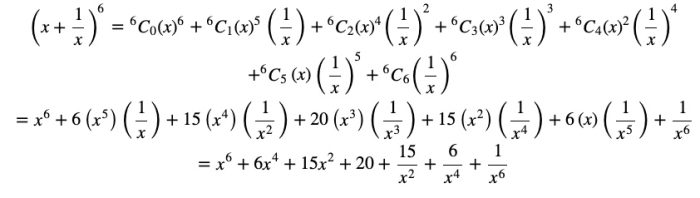
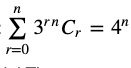

Leave a Reply