NCERT Solutions for Exercise 6.3, Class 11, Maths - Class 11, Maths, NCERT Solutions

Exercise 6.3
Permutations and combinations
Question and Answers
Class 11 – Maths

Class	Class 11
Subject	Mathematics
Chapter Name	Permutations and Combinations
Chapter No.	Chapter 6
Exercise	Exercise 6.3
Category	Class 11 Maths NCERT Solutions

Question 1 How many 3-digit numbers can be formed by using the digits 1 to 9 if no digit is repeated?

Answer Total number of digits possible for choosing = 9

Number of places for which a digit has to be taken = 3

As there is no repetition allowed , Number of permutations

= 9×8×7=504

Question 2 How many 4-digit numbers are there with no digit repeated?

Answer The thousands place of the 4-digit number can be filled with any digit from 1 to 9 and 0 is not included. Thus, number of ways in which thousands place is filled is 9.

The hundreds, tens and units place can be filled with any digit from 0 to 9.

Since, the digits cannot be repeated and thousands place is already occupied by the digit. The hundreds, tens and units place can be filled by remaining 9 digits.

Thus, there are permutations of 9 different digits taken 3 at a time.

Number of 3-digit numbers =

=9×8×7=504

Number of 4-digit numbers is $9 \times 504 = 4536$

Question 3 How many 3-digit even numbers can be made using the digits 1, 2, 3, 4, 6, 7, if no digit is repeated?

Answer The units place can be filled by any of the digits 2, 4 or 6. Hence, there are 3 ways.

Digits cannot be repeated and units place is already occupied so the hundreds and tens place can be occupied by remaining 5 digits.

Thus, number of ways of filling hundreds and tens place =

= 20

Therefore, the total number of permutations =3 × 20=60

Question 4 Find the number of 4-digit numbers that can be formed using the digits 1, 2, 3, 4, 5 if no digit is repeated. How many of these will be even?

Answer Total number of digits possible for choosing = 5

Number of places for which a digit has to be taken = 4

There are permutations of 5 different things taken 4 at a time.

Thus, number of 4 digit numbers =

= 1×2×3×4×5 = 120

Out of 1, 2, 3, 4, 5, we know that even numbers end either by 2 or 4.Thus, ways in which units place can be filled is 2.

Since, repetition is not allowed, units place is already occupied by a digit and remaining vacant places can be filled by remaining 4 digits.

Thus, number of ways in which remaining places can be filled =

=4×3×2×1 = 24

Number of even numbers = $24 \times 2 = 48$

Question 5 From a committee of 8 persons, in how many ways can we choose a chairman and a vice chairman assuming one person can not hold more than one position?

Answer In a committee of 8 persons, a chairman and vice chairman are selected in such away that one person can hold only one position.Thus, ways of choosing a chairman and vice chairman is permutation of 8 objects taken 2 at a time.

Therefore, number of ways

Question 6 Find n if ^n-1P₃: ⁿP₃ = 1: 9.

Answer

Question 7 Find r if

(i) ⁵P_r = 2⁶P_r-1

$\Rightarrow (7 - r) (6 - r) = 12$

$\Rightarrow 42 - 6 r - 7 r + r = 12$

$\Rightarrow r^{2} - 13 r + 30 = 0$

$\Rightarrow r^{2} - 3 r + 10 r + 30 = 0$

$\Rightarrow r^{2} - 3 r + 10 r + 30 = 0$ $\Rightarrow r (r - 3) - 10 (r - 3) = 0$

$\Rightarrow (r - 3) (r - 10) = 0$

$\Rightarrow r = 3 = 0$

$\Rightarrow r = 3$

$∴ 0 ⩽ r ⩽ 5$

$∴ r = 3$

(ii) ⁵P_r = ⁶P_r-1

$\Rightarrow (7 - r) (6 - r) = 6$

= $\Rightarrow 42 - 7 r - 6 r + r^{2} - 6 = 0$

$\Rightarrow r^{2} - 13 r + 36 = 0$

= $\Rightarrow r^{2} - 4 r - 9 r (r - 4) = 0$

$\Rightarrow (r - 4) (r - 9) = 0$

= $\Rightarrow (r - 4) (r - 9) = 0$

$\Rightarrow (r - 4) = 0 or (r - 9) = 0$

= $\Rightarrow r = 4 or r = 9$

Hence, $r \neq 9$

$∴ r = 4$

Question 8 How many words, with or without meaning, can be formed using all the letters of the word EQUATION, using each letter exactly once?

Answer The number of different letters in the given word is 8.

Thus, the number of words than can be formed without repetition is number of permutations of 8 different objects taken 8 at a time = $^{8} P_{8} = 8!$ = 8!

Therefore, number of words formed = 8! = 40320.

Question 9 How many words, with or without meaning can be made from the letters of the word MONDAY, assuming that no letter is repeated, if.

(i) 4 letters are used at a time,

(i) Number of different letters in the given word = 6

Number of 4-letter words that can be formed from the letters of the given word without repetition is permutations of 6 different objects taken 4 at a time.

Therefore, Number of 4 letter words that can be formed

(ii) all letters are used at a time,

(ii) Number of different letters in the given word = 6

Words that can be formed using all the letters of the given word is permutation of 6 different objects taken 6 at a time.

⁶P₆ = 6!

Therefore, number of words that can be formed is

$= 6! = 6 \times 5 \times 4 \times 3 \times 2 \times 1 = 720$

(iii) all letters are used but first letter is a vowel?

(iii) There are two different vowels in the word MONDAY which occupies the rightmost place of the words formed. Hence, there are 2 ways.

Since, it is without repetition and the rightmost place is occupied, the remaining five vacant places can be filled by 5 different letters. Hence, 5! Ways.

Therefore, number of words that can be formed = $5! \times 2 = 120 \times 2 = 240$

Question 10 In how many of the distinct permutations of the letters in MISSISSIPPI do the four I’s not come together?

Answer Total number of letters in MISSISSIPPI =11

I appears 4 times, S appears 4 times, P appears 2 times and M appears one time in the given word

Thus, number of permutations of the given word

We take that 4 I’s come together, and they are treated as 1 letter, ∴ Total number of letters=11 – 4 + 1 = 8

Number of permutations = 8! / 4! 2! = 840 ways

Therefore, total number of permutations where four I’s don’t come together = 34650-840=33810

Question 11 In how many ways can the letters of the word PERMUTATIONS be arranged if the

(i) words start with P and end with S,

(i) Total number of letters in PERMUTATIONS =12

The only repeated letter is T; 2times whereas the first and last letters of the word are fixed as P and S.Hence, 10 letters are left.

Therefore, required number of permutations =

(ii) vowels are all together,

(ii) There are $5$ vowels in the given word, each appearing only once.

Since they have to always occur together, they are treated as a single object for the time being. This single object together with the remaining 7 objects will account for 8 objects, in total.

These 8 objects in which there are 2 T’s can be arranged in 8! / 2! ways.

Corresponding to each of these arrangements, the 5 different vowels can be arranged in 5 !.

Therefore the required number of arrangements are :

( 8 ! × 5 ! ) / 2 ! =( 8 × 7 × 6 × 5 × 4 ×3× 2 × 120 ) / 2 = $\frac{8!}{2!} \times 5! = 2419200$

(iii) there are always 4 letters between P and S?

(iii) The letters have to be arranged in such a way that there are always 4 letters between P and S. Therefore, in a way, the places of P and S are fixed. The remaining 10 letters in which there are 2 T’s can be arranged in 10! / 2! ways.

Possible places of P & S are –

P and S can take the position 1 and 6

P and S can take the position 2 and 7

P and S can take the position 3 and 8

P and S can take the position 4 and 9

P and S can take the position 5 and 10

P and S can take the position 6 and 11

P and S can take the position 7 and 12

Also P & S can be interchanged as it won’t effect the number of letters between them.

So, the letters P and S can be placed such that there are 4 letters between them in 2 × 7 =14 ways.

Exercise 6.3 Permutations and combinations Question and Answers Class 11 – Maths

About Mrs Shilpi Nagpal

Reader Interactions

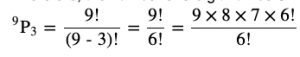
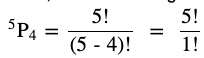
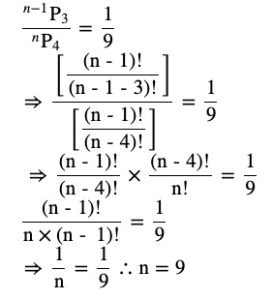
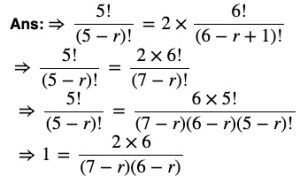
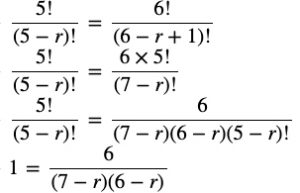
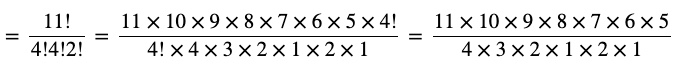
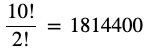
Leave a Reply

Exercise 6.3
Permutations and combinations
Question and Answers
Class 11 – Maths