Exercise 4.1
Complex Numbers and Quadratic Equations
Question and Answers
Class 11 – Maths
| Class | Class 11 |
| Subject | Mathematics |
| Chapter Name | Complex Numbers and Quadratic Equations |
| Chapter No. | Chapter 4 |
| Exercise | Exercise 4.1 |
| Category | Class 11 Maths NCERT Solutions |
Question 1 Express each of the complex number in the form a + ib.
(5i) (-3/5i)
Answer
(5i) (-3/5i)
= 5 x (-3/5) x i2
= -3 x -1 [i2 = -1]
= 3
(5i) (-3/5i) = 3 + i0
Question 2 Express the given complex number in the form a + ib
i9 + i19
Answer
i9 + i19 = (i2)4. i + (i2)9. i
= (-1)4 . i + (-1)9 .i
= 1 x i + -1 x i
= i – i
= 0
Hence,
i9 + i19 = 0 + i0
Question 3 Express the given complex number in the form a + ib
i-39
Answer
i−39 = i −4×9−3
=(i 4)−9 . i−3
=(1)−9 . i−3 [i4=1]
Question 4 Express the given complex number in the form a + ib
3 ( 7 + i 7) + i ( 7 + i 7 )
Answer
3(7 + i 7) + i (7 + i 7) = 21 +21 i + 7 i+ 7 i2
=21+28 i+7×(−1) [ i2=−1]
= 14 + 28 i
Question 5 Express the given complex number in the form a + ib
Answer
(1 – i ) – (–1 + i 6)
= (1−i)−(−1+ i 6)
= 1- i + 1 -6 i
2 – 7 i
Question 6 Express the given complex number in the form a + ib
Answer
Question 7 Express the given complex number in the form a + ib
Answer
Question 8 Express the given complex number in the form a + ib
(1 – i )4
Answer
(1 – i) 4 = [(1 – i)2]2
= [1 + i2 – 2i]2
= [1 – 1 – 2i]2 [i2 = -1]
= (-2i)2
= 4(-1)
= -4
Hence, (1 – i)4 = -4 + 0i
Question 9 Express the given complex number in the form a + ib
Answer
Question 10 Express the given complex number in the form a + ib
Answer
Question 11 Find the multiplicative inverse of given complex numbers 4 – 3i
Answer
Let z =4- 3i
z̄= 4 + 3i and | z | 2 = 42+(−3)2 = 16+9 = 25
Thus, the multiplicative inverse of 4 – 3i is given by z-1
Z -1 = z̄ / | z | 2
Z -1 = (4 + 3i) / 25
Z -1 = 4/25 + 3i /25
Question 12 Find the multiplicative inverse of the complex number √5 + 3i
Answer
z = √5 + 3i
z̄ = √5 – 3i
| z |2 = ( √5 )2 + 32
| z |2 = 14
Question 13 Find the multiplicative inverse of the complex number −i.
Answer
Let z=−i
Then, z̄ = i
| z |2 = 1
The multiplicative inverse of the complex number −i
Z -1 = z̄ / | z | 2
Z-1 = i / 1
Z-1 = 1
Question 14 Express the following expression in the form of a + ib :
Answer
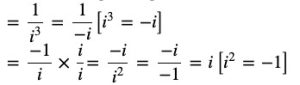
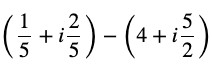
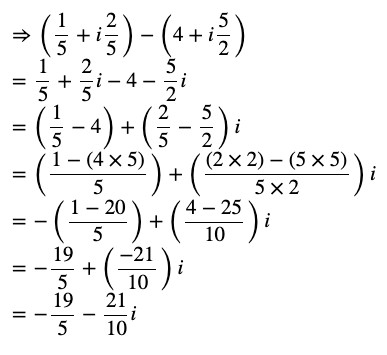
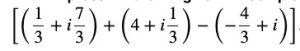
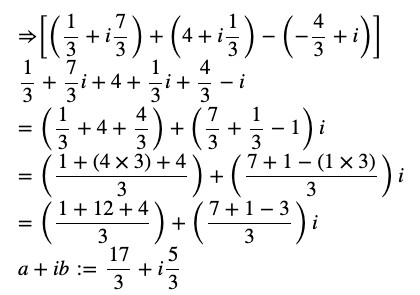
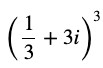
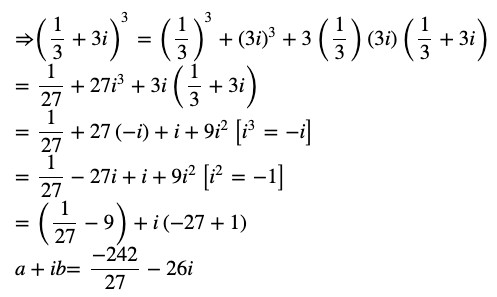
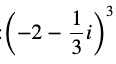
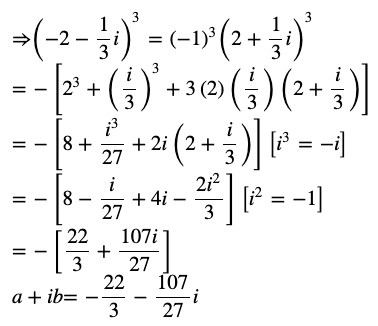
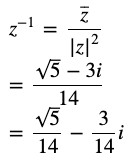
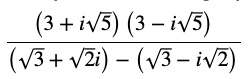
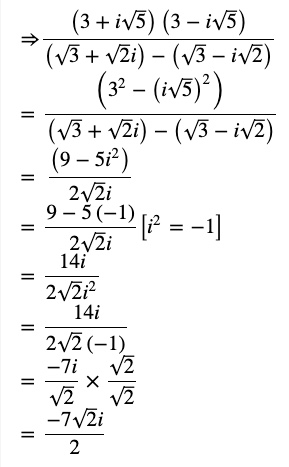
Leave a Reply