Exercise 3.3 Trigonometric Functions
Question and Answers
Class 11 – Maths
| Class | Class 11 |
| Subject | Mathematics |
| Chapter Name | Trigonometric Functions |
| Chapter No. | Chapter 3 |
| Exercise | Exercise 3.3 |
| Category | Class 11 Maths NCERT Solutions |
Question (1) Prove that
Answer
Question (2) Prove that
Answer
Question 3 Prove that
Answer
Question 4 Prove that
Answer
Question 5 Find the value of
(i) Sin 75°
Answer
Sin 75°= Sin ( 45°+ 30°)
Sin 75°= Sin 45° Cos 30° + Cos 45° Sin 30°
sin(x+y) = sin x cos y + cos x sin y
Therefore we have,
Question (5) Find the value of
(ii) tan 15°
Answer
tan 15°= tan ( 45°- 30° )
Question (6) Prove the following:
Answer
cos(x+y) = cos x cos y – sin x sin y
Question (7 ) Prove that
Answer
Question (8) Prove that
Answer
Observe that cos x repeats the same value after an interval
2 π and sin x repeats the same value after an interval 2 π
Question 9
Answer
We know that cot x repeats the same value after an interval 2π
Question (10) Prove that sin (n+1) x sin ( n+2 ) x + cos (n+1) x cos (n+2) x = cos x
Answer
cos(x-y) = cos x cos y + sin x sin y
L.H.S.= sin (n+1) x sin (n+2) x + cos (n+1) x cos (n+2) x
=cos [(n+1) x – ( n+2 ) x] = cos [ (n+1) x – (n+2) x]
=cos (-x)
=cos x
= R.H.S
Question (11) Prove that
Answer
Question (12) Sin26x – sin 2 4x = Sin 2x sin 10x
Answer
Question (13) cos2 2x – cos2 6x = sin 4x sin 8x
Answer
Question (14) sin2 x + 2 sin 4x + sin 6x = 4 cos2 x sin 4x
Answer
Question (15) cot 4x (sin 5x + sin 3x) = cot x (sin 5x – sin 3x)
Answer
Question (16)
Answer
Question (17)
Answer
Question (18)
Answer
Question (19) Prove that
Answer
Question (20) Prove that
Answer
Question (21)
Answer
Question (22) cot x cot 2x – cot 2x cot 3x – cot 3x cot x = 1
Answer
Question (23)
Answer
Question (24) cos 4x = 1 – 8sin2 x cos2 x
Answer
cos 2x = 1-2sin2x
And sin 2x=2sin x cos x
L.H.S.=cos 4x
=cos 2(2x)
=1-2sin22x
=1-2(2sin x cos x)2
L.H.S =1- 8sin2x cos2x
= R.H.S.
Hence proved.
Question (25) cos 6x = 32 cos6 x – 48cos4 x + 18 cos2 x – 1
Answer
cos 3A = 4cos3A – 3cosA
cos 2x= 1 – 2 sin2x
cos 2x = 2 cos2 x – 1
L.H.S. = Cos 6x = Cos cos 3(2x)
= 4 cos3 2x – 3 cos 2x
= 4 [(2 cos2 x – 1)3 – 3 (2 cos2 x – 1)
= 4 [(2 cos2 x) 3 – (1)3 – 3 (2 cos2 x) 2 + 3 (2 cos2 x)] – 6cos2 x + 3
= 4 [8cos6x – 1 – 12 cos4x + 6 cos2x] – 6 cos2x + 3
= 32 cos6x – 4 – 48 cos4x + 24 cos2 x – 6 cos2x + 3
= 32 cos6x – 48 cos4x + 18 cos2x – 1
= R.H.S
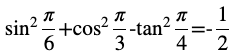
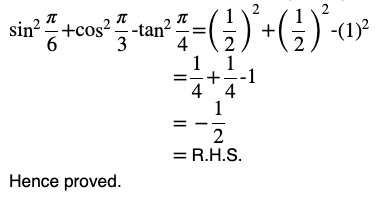
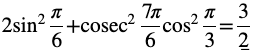

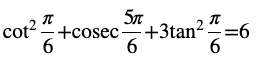


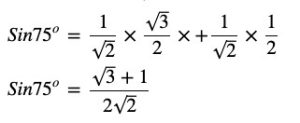
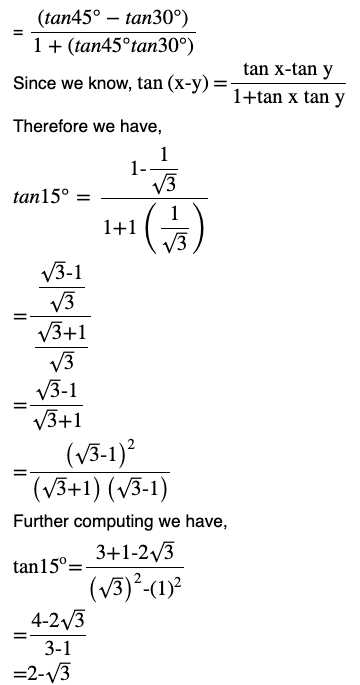
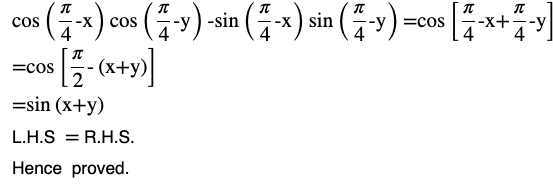
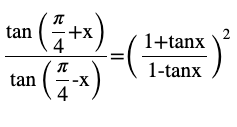

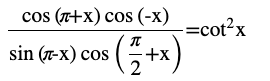
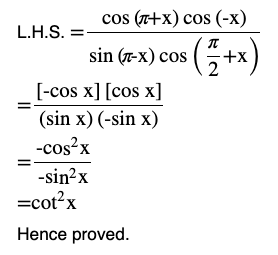
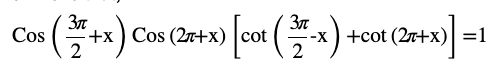
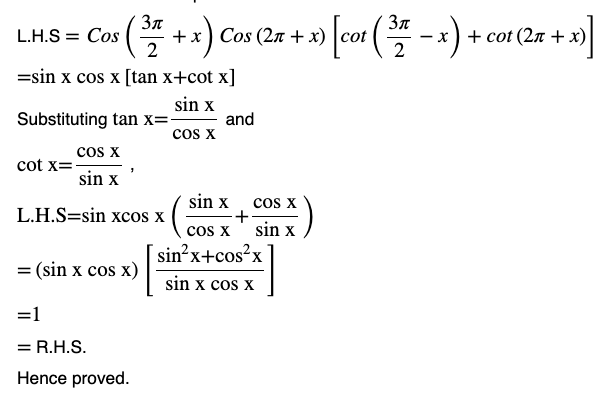
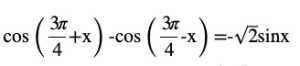

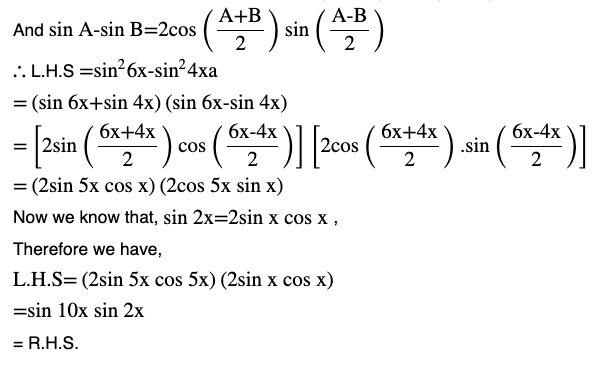



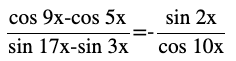

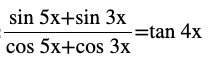

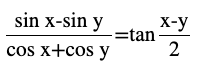

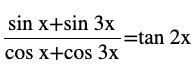

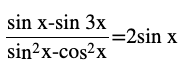
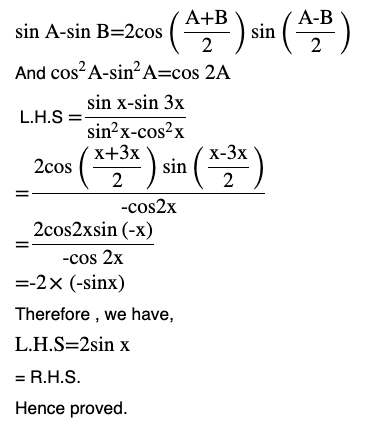
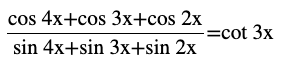


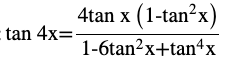
Leave a Reply