Exercise 3.2 Trigonometric Functions
Question and Answers
Class 11 – Maths
| Class | Class 11 |
| Subject | Mathematics |
| Chapter Name | Trigonometric Functions |
| Chapter No. | Chapter 3 |
| Exercise | Exercise 3.2 |
| Category | Class 11 Maths NCERT Solutions |
Question 1 Find the values of other five trigonometric functions if
(1) cos x = – 1 / 2 , x lies in third quadrant.
Answer
(1) Cos x = -1/2
sec x = -2
sin2x+cos2x=1
sin2x=1-cos2x
Substituting cos x = – 1/ 2 in the formula, we obtain,
sin2x = 1 – (-1/2)2
sin2x = 1 – (1/4)
sin2x = 3/4
Sin x = ±√ 3 / 2
Since x lies in the 3rd quadrant, the value of sin x will be negative.
Sin x = -√ 3 / 2
Cosec x = 1 / sin x
Cosec x = 1 / (- √ 3 / 2)
Cosec x = – 2 / √ 3
tan x = sin x / cos x
tan x = ( -√ 3 / 2 ) / (-1/2)
tan x = √3
cot x = 1/ tan x
cot x = 1 / √3
(2) sin x = 3/ 5 , x lies in second quadrant
Sin x = 3/5
cosec x = 1/ sin x
cosec x = 1 /(3/5)
cosec x = 5/3
sin2x+cos2x=1
cos2x=1- sin2x
Substituting sin x = 3 / 5 in the formula, we obtain,
cos2x=1 – (3/5)2
cos2x=1 – (9/25)
cos2x=16 /25
cos x = ± 4 / 5
Since x lies in the second quadrant, the value of cos x will be negative.
cos x = – 4 / 5
sec x = 1 / cos x
sec x = 1/ (-4/5)
sec x = – 5/4
tan x = sin x / cos x
tan x = (3/5) / (-4/5)
tan x = -3/ 4
cot x = 1 / tan x
cot x = 1 / (-3/4)
cot x = -4 /3
(3) cot x = 4/3 , x lies in third quadrant
cot x = 3/ 4
tan x = 1 / cot x
tan x = 4/3
sec2x – tan2x = 1
sec2x = 1+ tan2x
sec2x = 1+ (4/3)2
sec2x = 1+ (16 /9)
sec2x = 25 / 9
sec x = ± 5 / 3
Since x lies in the 3rd quadrant, the value of sec x will be
sec = – 5/3
cos x = 1 / sec x
cos x = 1 / (-5/3)
cos x = – 3/ 5
tan x = sin x/ cos x
sin x = tan x × cos x
sin x = ( 4/ 3) × ( – 3/ 5 )
sin x = – 4/ 5
cosec x = 1/ sin x
cosec x = -5/4
(4) sec x = 13/5 , x lies in fourth quadrant
sec x = 13 / 5
cos x = 1 /sec x
cos x = 1 /(13 /5 )
cos x = 5/ 13
sec2x – tan2x = 1
tan2x = sec2x – 1
tan2x = (13 / 5)2 – 1
tan2x = (169 / 25 ) -1
tan2x = 144 / 25
tan x = ± 12 / 5
Since x lies in the 4th quadrant the value of tan x will be negative.
tan x = -12/ 5
cot x = 1 / tan x
cot x = – 5 /12
tan x = sin x /cos x
sin x = tan x × cos x
sin x = (-12/ 5) × ( 5/13)
sin x= -12 /13
cosec x = 1 / sin x
cosec x =- 13 /12
(5) tan x = – 5 /12 , x lies in second quadrant.
tan x = – 5/12
cot x = 1 / tan x
cot x = 1 /(-5/12)
cot x = -12 /5
1 + tan2 x = sec2 x
We can write it as
1 + (-5/12)2 = sec2 x
Substituting the values
1 + 25/144 = sec2 x
sec2 x = 169/144
sec x = ± 13/12
Here x lies in the second quadrant so the value of sec x will be negative
sec x = – 13/12
cos x = 1 /sec x
cos x = – 12 /13
tan x = sin x/ cos x
sin x = tan x × cos x
sin x = (-5/12) × (-12 / 13)
sin x= 5 /13
cosec x= 1 / sin x
cosec x = 13 / 5
Find the values of the trigonometric functions in Exercises
(6) sin 765°
(6) We know that the values of sin x repeat after an interval of 2π or 360°
sin 765° = sin (2 × 360°+45°)
sin 765° = sin 45°
sin 765° = 1/ √2
(7) cosec (– 1410°)
(7) We know that the values of sin x repeat after an interval of 2π or 360°
cosec (-1410° ) = cosec (-1410°+4 × 360°)
= cosec(-1410°+1440°)
= cosec30°
= 2
(8) tan 19π /3
(8) We know that the values of sin x repeat after an interval of 2π or 360°
(9) sin (– 11π/ 3 )
(9) We know that the values of sin x repeat after an interval of 2π or 360°
(10) cot (– 15π/ 4 )
(10) We know that the values of sin x repeat after an interval of 2π or 360°
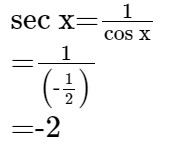
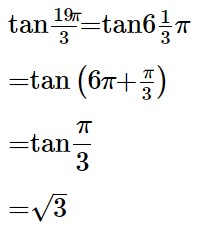
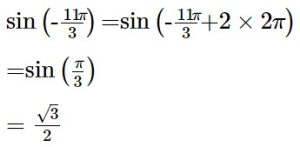
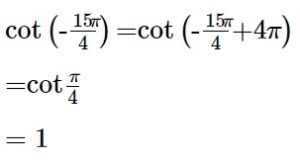
Leave a Reply