Exercise 3.1 Trigonometric Functions
Question and Answers
Class 11 – Maths
| Class | Class 11 |
| Subject | Mathematics |
| Chapter Name | Trigonometric Functions |
| Chapter No. | Chapter 3 |
| Exercise | Exercise 3.1 |
| Category | Class 11 Maths NCERT Solutions |
Question 1 Find the radian measures corresponding to the following degree measures:
Answer
Question 2 Find the degree measures corresponding to the following radian measures (Use π= 22/7 ).
Answer
Question 3 A wheel makes 360 revolutions in one minute. Through how many radians does it turn in one second?
Answer
No. of revolutions made by the wheel in 1 minute = 360
1 second = 360/60 = 6
The wheel turns an angle of 2π radian in one complete revolution.
In 6 complete revolutions, it will turn an angle of 6 × 2π radian = 12 π radian
Therefore, in one second, the wheel turns an angle of 12π radian.
Question 4 Find the degree measure of the angle subtended at the centre of a circle of radius 100 cm by an arc of length 22 cm (Use π= 22/7 ).
Answer
Here l = 22 cm and r = 100 cm
Using the formula
θ = 1/r, we have
⇒ θ = 22/100 = 11/50 rad (∵ θ = 1/r)
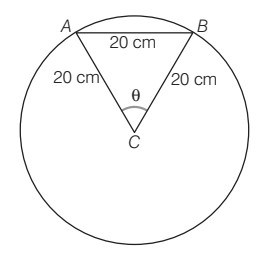
Question 5 In a circle of diameter 40 cm, the length of a chord is 20 cm. Find the length of minor arc of the chord.
Answer
Given, diameter = 40 cm
∴ Radius CA = CB = diameter/ 2 = 40/ 2 = 20 cm
Also, chord AB = 20 cm
Now, we have all the three sides of Δ ABC
equal so, it is an equilateral triangle.
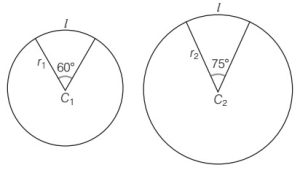
Question 6 If in two circles, arcs of the same length subtend angles 60° and 75° at the centre, find the ratio of their radii.
Answer
Firstly, determine the radii of both circles by using the formula θ = l/ r and then find their ratio.
Question 7 Find the angle in radian through which a pendulum swings if its length is 75 cm and the tip describes an arc of length
Answer
(i) 10 cm
(i) In a circle of radius r unit, if an arc of length l unit subtends an angle θ radian at the centre,
then θ = l /r
r = 75 cm , l = 10 cm
θ = 10/75 radian
θ = 2/15 radian
(ii) 15 cm
In a circle of radius r unit, if an arc of length l unit subtends an angle θ radian at the centre,
then θ = l /r
r = 75 cm , l = 15 cm
θ = 15/75 radian
θ = 1/15 radian
(iii) 21 cm
In a circle of radius r unit, if an arc of length l unit subtends an angle θ radian at the centre,
then θ = l /r
r = 75 cm , l = 21 cm
θ = 21/75 radian
θ = 7/25 radian





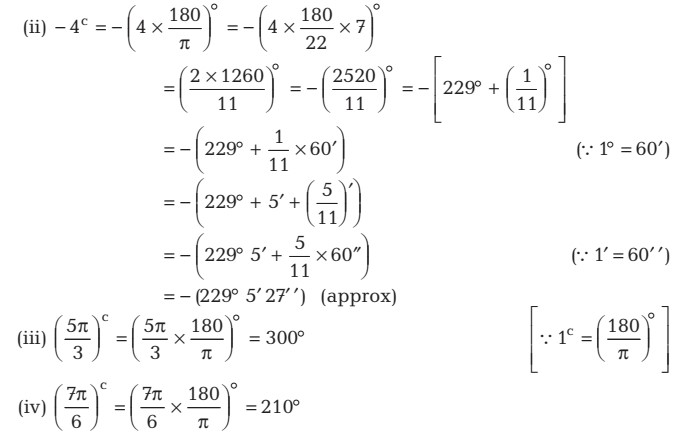
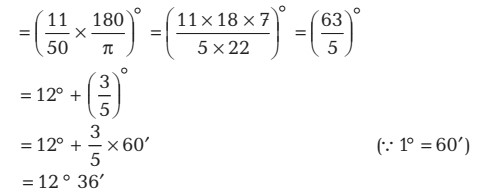
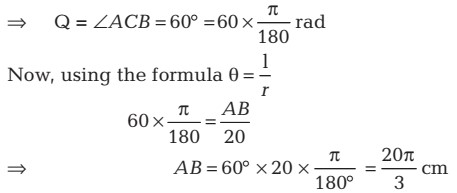
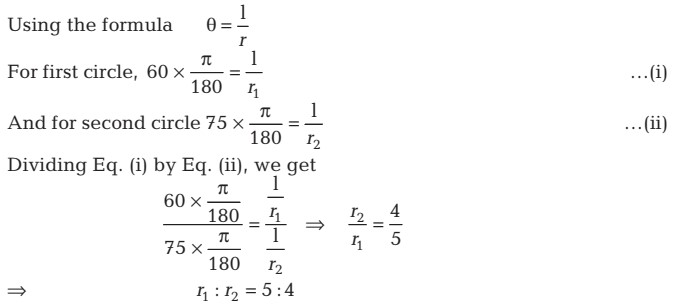
Leave a Reply