NCERT Solutions for Class 10 Maths
Chapter 2 Polynomials Exercise 2.4
Page 36
1. Verify that the numbers given alongside of the cubic polynomials below are their zeroes. Also verify the relationship between the zeroes and the coefficients in each case:
(i) 2x3+x2-5x+2; -1/2, 1, -2
(ii) x3-4x2+5x-2 ;2, 1, 1
(i) 2x3+x2-5x+2; -1/2, 1, -2
Given, p(x) = 2x3+x2-5x+2
And zeroes for p(x) are = 1/2, 1, -2
∴ p(1/2) = 2(1/2)3+(1/2)2-5(1/2)+2 = (1/4)+(1/4)-(5/2)+2 = 0
p(1) = 2(1)3+(1)2-5(1)+2 = 0
p(-2) = 2(-2)3+(-2)2-5(-2)+2 = 0
Hence, proved 1/2, 1, -2 are the zeroes of 2x3+x2-5x+2.
Now, comparing the given polynomial with general expression, we get;
∴ ax3+bx2+cx+d = 2x3+x2-5x+2
a=2, b=1, c= -5 and d = 2
As we know, if α, β, γ are the zeroes of the cubic polynomial ax3+bx2+cx+d , then;
α +β+γ = –b/a
αβ+βγ+γα = c/a
α βγ = – d/a.
Therefore, putting the values of zeroes of the polynomial,
α+β+γ = ½+1+(-2) = -1/2 = –b/a
αβ+βγ+γα = (1/2×1)+(1 ×-2)+(-2×1/2) = -5/2 = c/a
α β γ = ½×1×(-2) = -2/2 = -d/a
Hence, the relationship between the zeroes and the coefficients are satisfied.
(ii) x3-4x2+5x-2 ;2, 1, 1
Given, p(x) = x3-4x2+5x-2
And zeroes for p(x) are 2,1,1.
∴ p(2)= 23-4(2)2+5(2)-2 = 0
p(1) = 13-(4×12 )+(5×1)-2 = 0
Hence proved, 2, 1, 1 are the zeroes of x3-4x2+5x-2
Now, comparing the given polynomial with general expression, we get;
∴ ax3+bx2+cx+d = x3-4x2+5x-2
a = 1, b = -4, c = 5 and d = -2
As we know, if α, β, γ are the zeroes of the cubic polynomial ax3+bx2+cx+d , then;
α + β + γ = –b/a
αβ + βγ + γα = c/a
α β γ = – d/a.
Therefore, putting the values of zeroes of the polynomial,
α +β+γ = 2+1+1 = 4 = -(-4)/1 = –b/a
αβ+βγ+γα = 2×1+1×1+1×2 = 5 = 5/1= c/a
αβγ = 2×1×1 = 2 = -(-2)/1 = -d/a
Hence, the relationship between the zeroes and the coefficients are satisfied.
2. Find a cubic polynomial with the sum, sum of the product of its zeroes taken two at a time, and the product of its zeroes as 2, –7, –14 respectively.
Let us consider the cubic polynomial is ax3+bx2+cx+d and the values of the zeroes of the polynomials be α, β, γ.
As per the given question,
α+β+γ = -b/a = 2/1
αβ +βγ+γα = c/a = -7/1
α βγ = -d/a = -14/1
Thus, from above three expressions we get the values of coefficient of polynomial.
a = 1, b = -2, c = -7, d = 14
Hence, the cubic polynomial is x3-2x2-7x+14
3. If the zeroes of the polynomial x3-3x2+x+1 are a – b, a, a + b, find a and b.
We are given with the polynomial here,
p(x) = x3-3x2+x+1
And zeroes are given as a – b, a, a + b
Now, comparing the given polynomial with general expression, we get;
∴px3+qx2+rx+s = x3-3x2+x+1
p = 1, q = -3, r = 1 and s = 1
Sum of zeroes = a – b + a + a + b
-q/p = 3a
Putting the values q and p.
-(-3)/1 = 3a
a=1
Thus, the zeroes are 1-b, 1, 1+b.
Now, product of zeroes = 1(1-b)(1+b)
-s/p = 1-b2
-1/1 = 1-b2
b2 = 1+1 = 2
b = √2
Hence,1-√2, 1 ,1+√2 are the zeroes of x3-3x2+x+1.
4. If two zeroes of the polynomial x4-6x3-26x2+138x-35 are 2 ±√3, find other zeroes.
Given that 2 + √3 and 2 – √3 are zeroes of the given polynomial.
Therefore, (x-2-√3)(x-2+√3) = x2 + 4 − 4x − 3
= x2 − 4x + 1 is a factor of the given polynomial
For finding the remaining zeroes of the given polynomial, we will find the quotient by dividing x4-6x3-26x2+138x-35 by x2−4x + 1
Clearly, x4-6x3-26x2+138x-35 = (x2-4x+1)(x2-2x-35)
It can be observed that (x2-2x-35) is also a factor of the given polynomial.
And (x2-2x-35) = (x-7)(x+5)
Therefore, the value of the polynomial is also zero when x – 7 = 0 or x + 5 = 0
Or x = 7 or −5
Hence, 7 and −5 are also zeroes of this polynomial.
5. If the polynomial x4 – 6x3 + 16x2 – 25x + 10 is divided by another polynomial x2 – 2x + k, the remainder comes out to be x + a, find k and a.
By division algorithm,
Dividend = Divisor × Quotient + Remainder
Dividend − Remainder = Divisor × Quotient
x4-6x3+16x2-25x+10-x-a = x4-6x3+16x2-26x+10-a will be perfectly divisible by x2-2x+k
Let us divide x4-6x3+16x2-26x+10-a by x2-2x+k
It can be observed that (-10+2k)x + (10-a-8k+k2) will be 0
Therefore, (-10+2k) = 0 and (10-a-8k+k2) = 0
For (-10+2k) = 0,
2k =10
And thus, k = 5
For (10-a-8k+k2)= 0
10 − a − 8 × 5 + 25 = 0
10 − a − 40 + 25 = 0
− 5 − a = 0
Therefore, a = −5
Hence, k = 5 and a = −5
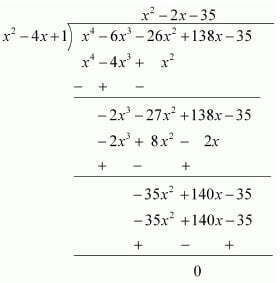
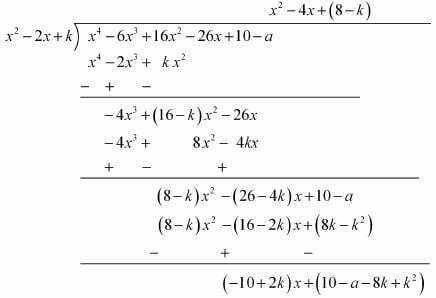
Leave a Reply